-
Distancia de seguridad mínima para evitar una colisión (1144)
Calcular la distancia de seguridad que debe dejar un conductor cuyo coche frena con una aceleración de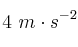 
si viaja a 
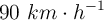y su tiempo de reacción es 0.8 segundos.
-
Composición de movimientos: perro que persigue a un conejo (1084)
Un conejo corre hacia su madriguera a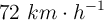 
. Cuando está a 200 m de ella un perro, situado 40 m detrás del conejo, sale en su persecución recorriendo 90 m con una aceleración de 
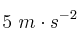y continuando después a velocidad constante.
a) ¿Alcanzará el perro al conejo?
b) ¿Qué ocurriría si la madriguera estuviera 100 m más lejos?
Razona ambas respuestas con ecuaciones.
-
UNED cinemática (1025)
Un barco navega por un río que tiene dirección norte-sur a 60 km/h con respecto a la orilla. Una corriente de 15 km/h le empuja desde el nordeste. ¿En qué dirección tiene que apuntar el barco para viajar en dirección norte?
-
Problema física relativista: velocidades relativas de los pasajeros de un tren (993)
Un tren lleva una velocidad constante de 90 km/h. Un viajero camina por el vagón, en el mismo sentido del movimiento del tren, a una velocidad de 0.5 m/s. En el otro extremo otro pasajero camina en sentido contrario a una velocidad de 0.68 m/s. Calcula:
a) La velocidad del primer viajero respecto de un observador situado fuera del tren.
b) La velocidad del segundo viajero respecto del mismo observador.
c) La velocidad del primer viajero con respecto al segundo.
-
Dinámica: aceleración y velocidad final en un plano inclinado (921)
El objeto del esquema se deja libre sobre el plano inclinado. Si el coeficiente de rozamiento en el plano inclinado es 0.15, calcula:
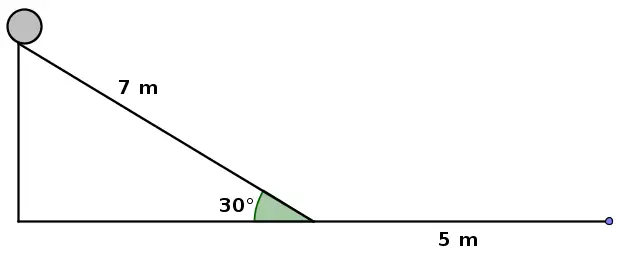
MRU
a) La aceleración a la que está sometida el objeto.
b) La velocidad del objeto al final del recorrido si sobre el tramo horizontal no hay rozamiento.
MRU
Ejercicios FyQ