Coeficiente de restitución

(2) ejercicios de Coeficiente de restitución

(#7428) Seleccionar

Conservación de energía en un choque con coeficiente de restitución distinto de uno (7428)

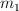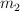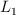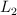Dos esferas de masas $m _1$ y $m _2$ están suspendidas de dos hilos paralelos de longitudes $L_1$ y $L_2$ respectivamente. En posición de equilibrio las esferas están con sus centros al mismo nivel. La masa 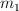$m _1$ se desvía lateralmente un ángulo 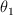$\theta _1$ y, a partir del reposo, se le deja en libertad. En su descenso choca con 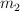$m _2$ y, tras el impacto se desviará un ángulo máximo 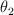$\theta _2$ . Si el coeficiente de restitución es e, determina:

a) Las velocidades de las esferas después de chocar.

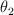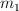b) El ángulo $\theta _2$ que $m _1$ se desvía tras el choque.
(#6665) Seleccionar

Velocidad tras un choque elástico y coeficiente de restitución (6665)

Una partícula de 300 g de masa se dirige hacia la derecha con una rapidez constante de 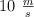$10 \ \textstyle{m\over s}$ . En sentido contrario, una partícula de 500 g de masa viaja con rapidez constante de 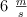$6 \ \textstyle{m\over s}$ . En un instante, las partículas chocan frontalmente y siguen separadas tras la colision. Si se sabe que durante el choque se disipo un 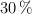$30 \%$ de la energía, calcula:

a) Las velocidades de las partículas inmediatamente después de la colisión.

b) El coeficiente de restitución.