-
EBAU Andalucía: física (junio 2010) - ejercicio B.3 (1489)
Por un plano inclinado que forma un ángulo de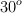 
con la horizontal se lanza hacia arriba un bloque de 10 kg con una velocidad inicial de 
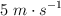. Tras su ascenso por el plano inclinado, el bloque desciende y regresa al punto de partida con una cierta velocidad. El coeficiente de rozamiento entre plano y bloque es 0.1.
a) Dibuja en dos esquemas distintos las fuerzas que actúan sobre el bloque durante el ascenso y durante el descenso e indique sus respectivos valores. Razona si se verifica el principio de conservación de la energía en este proceso.
b) Calcula el trabajo de la fuerza de rozamiento en el ascenso y en el descenso del bloque. Comenta el signo del resultado obtenido.
Dato: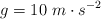 
-
Trabajo conservativo y no conservativo (1444)
Calcula el trabajo realizado por las fuerzas que actúan sobre un cuerpo que desliza sobre un plano inclinado un ángulo 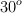como el que ves en la figura, sabiendo que su masa es 5 kg y el coeficiente de rozamiento dinámico es 0.2, cuando el cuerpo desciende 0.75 m por el plano:
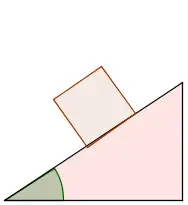
Fuerza rozamiento
-
Leyes de Newton: Fuerza de rozamiento (1410)
Los coeficientes de rozamiento entre los neumáticos de un automóvil y la calzada son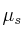 
= 0.6 y 
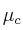= 0.5.
a) Si la fuerza resultante que se ejerce el vehículo es igual a la fuerza del rozamiento estático por la calzada, ¿cuál será la aceleración máxima del automóvil?
b) ¿Cuál será la distancia mínima de detención si la velocidad inicial del vehículo es de 30 m/s y no se produce derrape?
c) ¿Cuál será la distancia de detención si el vehículo derrapa y la fuerza de rozamiento es la producida por el coeficiente de rozamiento cinético?
-
Leyes de Newton: Fuerza de rozamiento (1409)
Una persona se coloca sobre un plano liso y comienza a deslizar por el plano cuando este alcanza una inclinación de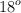 
. Determina el coeficiente de rozamiento entre el plano y la suela de los zapatos.
-
Leyes de Newton: Fuerza de rozamiento (1408)
El coeficiente de rozamiento estático entre una caja y la superficie de un plano inclinado es 0.4. ¿Cuál será el valor máximo del ángulo del plano para que la caja no deslice sobre él?
Fuerza rozamiento
Ejercicios FyQ