-
Energía potencial gravitatoria (1432)
Un péndulo simple de longitud L es desplazado de su posición de equilibrio hasta formar un ángulo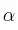 
y luego se suelta. Determina la velocidad del péndulo y la tensión del hilo en el punto más bajo de la trayectoria.
-
Energía mecánica y conservación de la energía en las colisiones (1313)
Un coche, que denominaremos coche 1, se encuentra en lo alto de una cuesta de 1 000 m de longitud y a una altura de 50 m. La masa del coche es de 2 000 kg. Se le suelta el freno de mano y comienza a descender por la carretera que posee un coeficiente de rozamiento dinámico de 0.02. Al final de la cuesta choca inelásticamente contra el coche 2, de 1 500 kg de masa, que está parado. A 50 m de distancia del choque se encuentra el coche 3, de 1 000 kg de masa. Si el coeficiente de rozamiento en el llano es de 0.1; determina:
a) La energía potencial del coche 1 en el punto donde se le soltó el freno de mano.
b) Energía cinética del coche 1 antes de chocar con el coche 2.
c) ¿Chocan el conjunto coche 1 y 2 con el coche 3?
d) Si el choque de 1+2 con 3 es perfectamente elástico, ¿qué distancia recorre el coche 3 antes de pararse por rozamiento?
-
UNED trabajo y energía 0004
Una caja desliza sobre un suelo de madera pulido con una velocidad de 5 m/s. Si se detiene tras recorrer 10 m, ¿cuál será el coeficiente de rozamiento entre suelo y caja?
-
UNED trabajo y energía 0003
Dos niños de 30 y 35 kg respectivamente se lanzan en un mismo trineo (de masa 3 kg) por una ladera nevada, que mide 60 m de largo y forma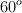 
con la horizontal. El coeficiente de rozamiento es de 0.3. Calcule:
a) El trabajo efectuado por todas la fuerzas en el tramo de bajada.
b) La velocidad del trineo al final de la cuesta.
c) Los niños vuelven a subir la ladera tirando del trineo, ¿qué trabajo efectúan?
-
UNED trabajo y energía 0002
Un bloque de 2 kg desliza por una rampa sin rozamiento desde una altura de 3 m. ¿Qué velocidad llevará el bloque en la base de la rampa?
Conservación energía
Ejercicios FyQ