-
Aceleración mínima para poder tomar el autobús (6815)
María salió de su casa apurada porque llegaba tarde a sus prácticas. Parte del reposo y empieza a caminar con una aceleración constante de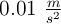 
. Cuando recorrió 5 m cruzó la calle y vio detrás de ella, a 320 m de distancia, al autobús acercándose a una velocidad constante de 
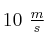, así que decide acelerar para alcanzarlo. Si la distancia desde ese punto a la parada es de 100 m, ¿cuál tiene que ser la aceleración mínima que debe adoptar María cuando cruza la calle para poder llegar a tiempo a la parada y tomar el autobús?
-
Velocidad de un coche cuando alcanza a un camión (6802)
Un camión que se desplaza a velocidad constante de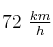 
adelanta a un coche que se encuentra parado en la carretera. Si este arranca 6 s después con una aceleración constante de 
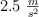calcula la velocidad del coche cuando alcanza al camión, expresada en 
.
-
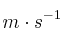Distancia que separa a dos vehículos cuando uno empieza a frenar (6726)
Dos automóviles A y B están uno junto al otro, viajan en la misma dirección y con la misma rapidez. Si B mantiene su rapidez constante, mientras que A empieza a desacelerar, ¿cuál será la distancia que separará a ambos automóviles en el instante en el que A se detiene?
-
Aceleración mínima de dos vehículos para que no choquen (6718)
Dos móviles se encuentran inicialmente separados por una distancia F. El móvil 1 se mueve de izquierda a derecha con una rapidez inicial de 20 m/s y una aceleración de frenado desconocida. El móvil 2 sale 1.5 s más tarde, de derecha a izquierda, con rapidez inicial de 15 m/s y una aceleración de frenado desconocida pero igual en modulo a la del móvil 1:
a) Realiza el esquema de la situación indicando el sistema de referencia utilizado y dibuja los vectores velocidad y aceleración correspondientes.
b) Calcula el valor de aceleración mínimo que deben tener los móviles para que no se produzca el choque, de forma que logren detenerse justo al llegar al encuentro.
c) Calcula el valor de la distancia F para esa situación extrema.
-
Cuerpo que cae libremente y desciende hasta el fondo de un pozo
Un cuerpo se deja caer en el vacío desde una altura L. Se sabe que en su caída pasa cerca de un cuadro de 1 m de altura, recorriéndolo en 0.25 s. A partir de que termina de cruzar el cuadro se toma otros 3.55 s para llegar al nivel del suelo, donde se encuentra un pozo de profundidad K. Desde el momento en el que cruza la boca del pozo hasta que se escucha el sonido del golpe de la piedra con el fondo pasan 4 s, siendo la velocidad del sonido de 330 m/s. Halla:
a) La altura L desde la que se deja caer la piedra.
b) El instante en el que llega al suelo.
c) La altura a la que se halla el comienzo del cuadro (marco superior del mismo).
d) La profundidad K del pozo.
Composición movimientos
Ejercicios FyQ