-
Acceso25 septiembre 2012: Conservación de la cantidad de movimiento (2005)
Un niño de 35 kg desliza con su monopatín a 20 km/h. De repente, un amigo suyo de 40 kg de masa se sube al monopatín. Si no se dan ningún impulso, ¿a qué velocidad irá el monopatín con los dos niños encima?
-
Masa máxima de una piedra para que la cuerda no se rompa al girar (1970)
Un niño hace girar una piedra atada a una cuerda haciendo una circunferencia vertical. La máxima tensión que aguanta la cuerda es de 245 N. Si la cuerda mide 120 cm y la velocidad a la que hace girar la piedra es de 14 m/s, ¿qué masa máxima puede tener la piedra para que no se rompa la cuerda? Dibuja todas las fuerzas que actúan sobre el sistema.
-
Dinámica y energía: selectividad Andalucía junio 2012
Un cuerpo de 5 kg, inicialmente en reposo, se desliza por un plano inclinado de superficie rugosa que forma un ángulo de 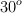 con la horizontal, desde una altura de 0.4 m. Al llegar a la base del plano inclinado, el cuerpo continúa deslizándose una superficie horizontal rugosa del mismo material que el plano inclinado. El coeficiente de rozamiento dinámico entre el cuerpo y las superficies es de 0.3.
con la horizontal, desde una altura de 0.4 m. Al llegar a la base del plano inclinado, el cuerpo continúa deslizándose una superficie horizontal rugosa del mismo material que el plano inclinado. El coeficiente de rozamiento dinámico entre el cuerpo y las superficies es de 0.3.
a) Dibuja en un esquema las fuerzas que actúan sobre el cuerpo en su descenso por el plano inclinado y durante su movimiento a lo largo de la superficie horizontal. ¿A qué distancia de la base del plano se detiene el cuerpo?
b) Calcula el trabajo que realizan todas las fuerzas que actúan sobre el cuerpo durante su descenso por el plano inclinado.
Dato: 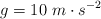
-
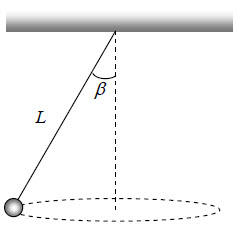
Deducción de la ecuación de la velocidad angular en un péndulo cónico (1789)
Una partícula de masa m (kg) que pende de un hilo inextensible, de longitud L (m), se mueve en un círculo horizontal con rapidez constante, v 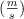 , constituyendo un péndulo cónico. Suponiendo que se conoce el ángulo
, constituyendo un péndulo cónico. Suponiendo que se conoce el ángulo 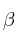 , que forma el hilo con la vertical, demuestra que la velocidad angular,
, que forma el hilo con la vertical, demuestra que la velocidad angular, 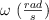 , puede ser calculada mediante la ecuación:
, puede ser calculada mediante la ecuación:
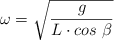
donde g es la magnitud de la aceleración de la gravedad 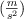 .
.
Dinámica
-
Peso específico del agua almacenada en un depósito (1780)
Se dispone de un depósito cilíndrico para almacenar agua. El diámetro de dicho depósito es de 10 m y tiene una altura de 100 m. Calcula el volumen de agua que puede almacenar. ¿Cuál es el peso específico del agua contenida en el volumen cilíndrico? (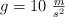 ).
).
 Dinámica
Dinámica