Ejercicios Resueltos, Situaciones de aprendizaje y VÍDEOS de Física y Química para Secundaria y Bachillerato
Últimos Ejercicios Publicados
-
[P(520)] Análisis de la espontaneidad de una reacción química (8408)
19 de marzo, por F_y_QPuedes hacer clic en este enlace para ver el enunciado y las respuestas del problema que se resuelve en el vídeo.
-
Energía liberada en la fisión del uranio-235 y reacción de fisión nuclear (8416)
18 de marzo, por F_y_QUn núcleo de uranio-235 (
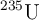 ) experimenta una fisión nuclear y se divide en dos fragmentos, uno de los cuales es kriptón-92 (
) experimenta una fisión nuclear y se divide en dos fragmentos, uno de los cuales es kriptón-92 (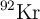 ) y el otro es bario-141 (
) y el otro es bario-141 (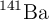 ). Además, se emiten tres neutrones (3n) en el proceso.
). Además, se emiten tres neutrones (3n) en el proceso.a) Escribe la ecuación nuclear que describe esta reacción de fisión.
b) Calcula la energía liberada en esta reacción, expresada en MeV.
Datos:
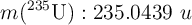 ;
; 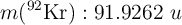 ;
; 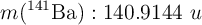 ;
; 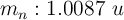 ;
; 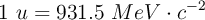
-
Desintegración alfa, energía liberada y energía cinética de la partícula alfa (8417)
17 de marzo, por F_y_QUn núcleo de plutonio-239 (
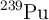 ) experimenta una desintegración alfa y se transforma en uranio-235
) experimenta una desintegración alfa y se transforma en uranio-235 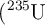 ).
).a) Escribe la ecuación nuclear que describe esta desintegración alfa.
b) Calcula la energía cinética total liberada en la desintegración, expresada en MeV.
c) Suponiendo que el núcleo de uranio-235 y la partícula alfa comparten la energía liberada, calcula la energía cinética de la partícula alfa.
Datos:
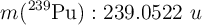 ;
; 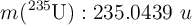 ;
; 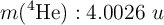 ;
; 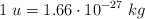 ;
; 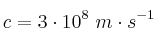
-
Posición, velocidad, momento lineal y aceleración del centro de masas de un sistema de dos partículas (8415)
15 de marzo, por F_y_QUn sistema de dos partículas de masas 2 y 3 kg se mueven en el plano XY. En un instante dado, las posiciones y velocidades de las partículas son:
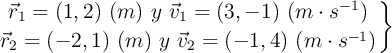
a) Calcula la posición del centro de masas (CM) del sistema.
b) Determina la velocidad del centro de masas.
c) Calcula el momento lineal total del sistema.
d) Determina el momento angular total del sistema respecto al origen.
e) Si las partículas están sometidas a las fuerzas externas
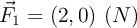 y
y 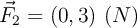 , calcula la aceleración del centro de masas.
, calcula la aceleración del centro de masas. -
Ecuación de dimensiones del momento de inercia y homogeneidad de algunas fórmulas (8414)
14 de marzo, por F_y_QDetermina la ecuación de dimensiones del momento de inercia y comprueba la homogeneidad de las siguientes fórmulas físicas:
a)
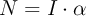
b)
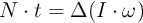
c)
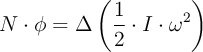
donde «N» es el momento del par, «I» es el momento de inercia, «t» es el tiempo y «
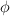 », «
», «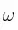 » y «
» y «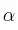 » son, respectivamente, el ángulo de giro, la velocidad angular y la aceleración angular.
» son, respectivamente, el ángulo de giro, la velocidad angular y la aceleración angular.
 Ejercicios FyQ
Ejercicios FyQ