-
Tiempo y posición en la que se cruzan dos corredores que se mueven en sentido contrario
Por un extremo de una pista rectilínea de carreras pasa un primer corredor que se mueve hacia la derecha con una velocidad constante de 18 km/h. En ese mismo instante pasa por el extremo opuesto un segundo corredor que se mueve hacia la izquierda y lleva una velocidad constante de 1 m/s. Sabiendo que la pista tiene una longitud de 1 km, determina el instante y la posición en que se cruzan ambos corredores.
-
Tiempo de vuelo y velocidad inicial de un obús sabiendo su alcance y ángulo
Se quiere alcanzar un objetivo a 12 km de distancia con un obús de 105 mm. El ángulo de elevación del disparo es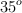 
:
a) ¿Qué tiempo estará el proyectil en el aire?
b) ¿Cuál es la velocidad con la que fue lanzado?
-
Ecuaciones del movimiento de un lanzamiento oblicuo desde un edificio (6339)
Desde lo más alto de un edificio de 50 m de altura se lanza un cuerpo oblicuamente hacia arriba con una velocidad inicial de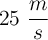 
en una dirección que forma un ángulo 
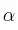con la horizontal, tal que 
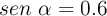y 
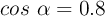. Suponiendo nula la resistencia del aire y que la aceleración de la gravedad es de 
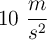, determina:
a) El vector de posición del móvil en función del tiempo.
b) En qué punto chocará con el suelo, supuesto horizontal.
c) La velocidad del móvil en función del tiempo.
d) Su velocidad en el instante del choque con el suelo.
e) La altura máxima que alcanzará el móvil en su recorrido.
f) La ecuación de la trayectoria de este movimiento.
-
Proyectil lanzado parabólicamente desde un edificio a otro (6338)
Desde la azotea de un edificio de 50 pisos (2 metros de altura por piso), se lanza un proyectil con un ángulo de inclinación de 
con respecto a la horizontal, con el propósito de impactar en la azotea de un edificio de 23 pisos (2 metros de altura por piso), que se encuentra alejado 500 metros y, para que el proyectil no sea detectado por las defensas del edificio, este debe durar en el aire 13.5 segundos como máximo.
Con la información suministrada y efectuando los procesos matemáticos correspondientes, responde a las preguntas siguientes:
a) ¿Cuál es la velocidad de lanzamiento del proyectil para lograr el objetivo?
b) ¿Cuál es la velocidad con la que impacta el proyectil contra la azotea del edificio de 23 pisos?
c) ¿Cuál es la altura máxima alcanzada por el proyectil desde su lanzamiento?
d) ¿Cuál es el ángulo de impacto del proyectil con respecto a la vertical?
e) ¿Cuál es el tiempo que tarda el proyectil en lograr su altura máxima?
f) ¿Cuál es la velocidad con la que el proyectil efectúa su trayectoria horizontal?
g) ¿Cuál es el tiempo que tarda el proyectil en caer desde su punto de máxima altura hasta lograr el objetivo?
-
Lanzamiento horizontal de provisiones desde una avioneta (6272)
Una avioneta vuela horizontalmente a 2 000 m de altura con una rapidez de 200 km/h. La misión del piloto es dejar un equipaje de provisiones a un grupo de personas aisladas por la inundación debido al fenómeno del niño en el mes de enero de 1988 en la costa ecuatoriana.
a) ¿A qué distancia antes de estar sobre el grupo debe soltar las provisiones?
b) ¿Qué rapidez tiene el equipaje a los 10 s del descenso?
c) ¿Con qué rapidez impacta en el suelo, si el equipaje no dispusiera de paracaídas?
Composición movimientos
Ejercicios FyQ