MCU

(50) ejercicios de MCU

(#1789) Seleccionar

Deducción de la ecuación de la velocidad angular en un péndulo cónico (1789)

Una partícula de masa m (kg) que pende de un hilo inextensible, de longitud L (m), se mueve en un círculo horizontal con rapidez constante, v 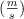$(\textstyle{m\over s})$ , constituyendo un péndulo cónico. Suponiendo que se conoce el ángulo 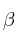$\beta$ , que forma el hilo con la vertical, demuestra que la velocidad angular, 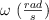$\omega\ (\textstyle{rad\over s})$ , puede ser calculada mediante la ecuación:

$\omega = \sqrt{\frac{g}{L\cdot cos\ \beta}}$

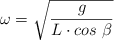
donde g es la magnitud de la aceleración de la gravedad 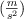$(\textstyle{m\over s^2})$ .

MCU
(#1407) Seleccionar

Ángulo del peralte de una curva para que sea segura tomarla (1407)

Una curva de 30 m de radio tiene un peralte de ángulo «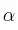 $\alpha$ ». Calcula el valor de « 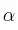$\alpha$ » para que un coche pueda tomar la curva a 40 km/h considerando que no existe rozamiento entre los neumáticos y la calzada.
(#1406) Seleccionar

Velocidad máxima para una curva sin peralte (1406)

Un coche toma una curva sin peralte que tiene un radio de 30 m. Si el coeficiente de rozamiento entre los neumáticos y el asfalto es 0.6, ¿cuál es la velocidad máxima a la que puede tomar la curva sin que derrape?
(#1405) Seleccionar

Leyes de Newton: Movimiento circular 0003

Las aspas de un ventilador tienen una longitud de 25 cm y completan 600 vueltas por minuto. Calcula la fuerza que ejerce una de ellas sobre un insecto de 1,2 g que se introduce perpendicularmente a la dirección de giro e impacta en el extremo de ésta.
(#1404) Seleccionar

Leyes de Newton: dinámica del movimiento circular (1404)

Si giramos un cubo atado a una cuerda de manera que describa una circunferencia vertical de radio «r» y en el punto más alto de la trayectoria su velocidad es «v», ¿cuál es la fuerza que ejerce el cubo sobre el agua que contiene? Determina el valor mínimo de «v» para que el agua no caiga.