-
Aceleración de frenada y fuerza de los frenos de un coche que para (1110)
Un coche de 1 100 kg circula a una velocidad de 80 km/h y ve una señal de «Stop» a 150 m. Comienza a reducir la marcha en ese instante y se detiene en 18 s. Calcula la aceleración de frenada y la fuerza ejercida por los frenos.
-
Lanzamiento vertical hacia arriba de una pelota desde una ventana (1088)
Un niño lanza hacia arriba una pelota desde el balcón de su casa que está a una altura de 7 m. Sabiendo que la pelota sube durante 0.3 s, determina:
a) La velocidad con la que el niño lanza la pelota hacia arriba.
b) La altura máxima que alcanza la pelota.
c) El tiempo transcurrido hasta que la pelota toca el suelo.
d) La velocidad con la que la pelota llega al suelo.
-
Desplazamiento, distancia y velocidad de un móvil, sabiendo su ecuación de la posición (1090)
El vector de posición de una partícula es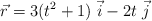 
. Calcula:
a) Los vectores de posición para los instantes 1 y 2 s.
b) El vector desplazamiento y la distancia entre ambas posiciones.
c) La velocidad de la partícula.
d) ¿Qué tipo de movimiento es?
-
Composición de movimientos: perro que persigue a un conejo (1084)
Un conejo corre hacia su madriguera a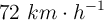 
. Cuando está a 200 m de ella un perro, situado 40 m detrás del conejo, sale en su persecución recorriendo 90 m con una aceleración de 
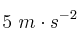y continuando después a velocidad constante.
a) ¿Alcanzará el perro al conejo?
b) ¿Qué ocurriría si la madriguera estuviera 100 m más lejos?
Razona ambas respuestas con ecuaciones.
-
Ecuación que permite conocer la posición de un objeto lanzado hacia arriba (994)
Una persona se encuentra 15 m por encima de otra cuando lanza hacia arriba un objeto con velocidad inicial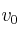 
. ¿Cuál es la ecuación de transformación que permite conocer la posición del objeto en cualquier instante para cualquiera de los dos observadores?
MRUA
Ejercicios FyQ