-
Ampliación: Fuerza necesaria para detener una objeto si se duplica su velocidad (7979)
Para detener en 20 m a cierto objeto que se desplaza a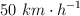 
, es necesario aplicarle una fuerza constante de 2 000 N en sentido contrario a su velocidad inicial. Si el mismo objeto se moviera a 
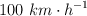y se quisiera detener en la misma distancia, ¿cuál sería la fuerza a aplicar?
-
Aceleración de un bloque se que empuja, cuando hay rozamiento (7893)
Considera un cuerpo de 6 kg de masa que está en reposo sobre un plano horizontal rugoso, cuyo coeficiente de rozamiento es 0.3. Una fuerza horizontal de 30 N actúa sobre él. Determina:
a) La aceleración del cuerpo.
b) La reacción del plano de apoyo.
-
Aceleración que adquiere un bloque que roza al que se aplica una fuerza (7855)
Un bloque de 40 N de peso, inicialmente en reposo sobre una superficie horizontal, se somete a la acción de una fuerza paralela a la superficie de 150 N. Si el coeficiente de fricción de la superficie de contacto es 0.2, determina la aceleración del bloque.
-
Impulso mecánico y fuerza sobre una pelota de béisbol (7844)
Una pelota de beisbol de 150 g, que se mueve hacia el bateador a una velocidad de 30 m/s, es golpeada con un bate, lo cual le provoca una velocidad de 42 m/s en dirección contraria a la inicial. Determina:
a) El impulso sobre la pelota.
b) La fuerza media ejercida sobre la pelota si el bate estuvo en contacto con ella durante 0.002 s.
-
Dinámica de traslación y rotación en un sistema de cuerpos enlazados (7724)
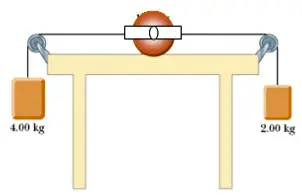
En la figura se muestra un sistema conformado por dos masas colgantes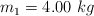 
, 
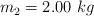, dos poleas de radio 
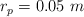y masa 
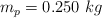fijadas en los extremos de la mesa y un disco de radio 
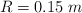y masa 
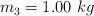. Los tres objetos se unen mediante una cuerda que pasa sin deslizarse por las poleas, cuyos ejes carecen de fricción, y se unen al disco por medio de un eje central que le permite rodar libremente sobre una mesa con superficie rugosa. Si el sistema se libera a partir del reposo, halla lo siguiente:
a) El valor de la aceleración del centro de masa del disco.
b) El valor de la rapidez final que alcanza la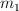 
si recorre 1 m sobre la mesa.
c) El valor de todas las tensiones del sistema.
Dinámica
Dinámica
Ejercicios FyQ