-
Ecuación de una onda y momento en el que un punto tiene velocidad nula (8121)
Una onda se propaga por la parte negativa del eje X con una longitud de onda de 20 cm, una frecuencia de 25 Hz, una amplitud de 3 cm y fase inicial igual a cero. Escribe la ecuación de la onda e indica el instante en el que un punto que se encuentra a 2.5 cm del origen alcanza, por primera vez, una velocidad nula.
-
EBAU Andalucía: física (junio 2022) - ejercicio C.1 (7892)
a) ¿Qué significa que una onda armónica es doblemente periódica? Explícalo apoyándote en las gráficas correspondientes.
b) Una onda armónica transversal se propaga en sentido negativo del eje OX con una velocidad de propagación de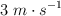 
. Si su longitud de onda es de 1.5 m y su amplitud es de 2 m: i) escribe la ecuación de la onda teniendo en cuenta que en el punto x = 0 m y en el instante t = 0 s la perturbación es nula y la velocidad de oscilación es positiva. ii) Determina la velocidad máxima de oscilación de un punto cualquiera del medio.
-
Ecuación de una onda electromagnética y dirección del campo magnético (7801)
Una onda electromagnética plana, que está polarizada, tiene un campo eléctrico de amplitud 3 N/C y una frecuencia de 1 MHz.
a) Determina la ecuación de onda que representa al campo eléctrico si la onda se propaga en el eje Y, estando el campo polarizado en el eje Z.
b) Calcula la dirección de polarización del campo magnético.
-
Ecuación de una onda con sentido negativo de propagación (7777)
Escribe la ecuación de una onda que se propaga en una cuerda (en sentido negativo del eje X) y que tiene las siguientes características: 0.5 m de amplitud, 250 Hz de frecuencia, 200 m/s de velocidad de propagación y la elongación inicial en el origen es nula. Determina la máxima velocidad trasversal de un punto de la cuerda.
-
Ecuación de la posición y velocidad de una onda a partir de gráficas (7776)
En las figuras se representa la variación de la posición (y) de un punto de una cuerda vibrante en función del tiempo (t) y de su distancia (x) al origen, respectivamente.
a) Deduce la ecuación de onda.
b) Determina la velocidad de propagación de la onda y la velocidad de vibración de un punto de la cuerda.
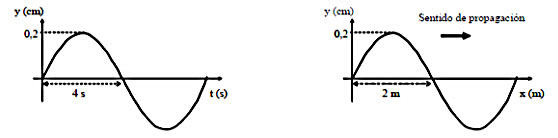
Función onda
Función onda
Ejercicios FyQ