-
Análisis del movimiento armónico simple de un partícula (6535)
Una partícula que se mueve describiendo un MAS durante un tiempo de 18 s. Tiene la siguiente ecuación (en unidades SI):
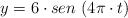
a) Halla el periodo del movimiento.
b) Halla la frecuencia.
c) Halla la elongación (x).
d) Halla el valor de la aceleración.
e) Si duplica el tiempo que tarda para dar una oscilación completa, ¿qué sucede con la elongación?
f) Si cuadruplico el valor de la masa que está oscilando, ¿qué pasa con la velocidad?
-
Ecuación del movimiento y distancia a un punto en función del tiempo de un oscilador armónico
Una partícula describe un movimiento armónico simple sobre el eje X. El centro de oscilación se halla en el eje de origen de coordenadas, la amplitud es 2 m y el periodo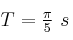 
. La posición en el instante inicial es (x = 2 m, y = 0).
a) Halla la ecuación del movimiento (posición en función del tiempo).
b) Halla la distancia de la partícula al punto (x = 0, y = 2 m) en función del tiempo.
-
PAU Andalucía septiembre 2012: Movimiento armónico simple
a) Escribe la ecuación de un movimiento armónico simple y explica cómo varían con el tiempo la velocidad y la aceleración de la partícula.
b) Comenta la siguiente afirmación: "si la aceleración de una partícula es proporcional a su desplazamiento respecto de un punto y de sentido opuesto, su movimiento es armónico simple".
-
Cuestión movimiento armónico simple 0001
Define el movimiento armónico simple e indica la ecuación que define la posición "x" en cualquier instante.
-
Oscilador armónico simple 0002
Un resorte vertical tiene una constante de recuperación de 1500 N/m y está unido a un objeto de masa «m». Cuando desplazamos el sistema 3 cm de su posición de equilibrio y lo soltamos, su frecuencia de oscilación es 7 Hz.
a) Calcula el valor de «m»
b) Determina el alargamiento del resorte cuando el sistema está en equilibrio.
c) Escribe las ecuaciones de la posición, velocidad y aceleración en función del tiempo.
Elongación
Ejercicios FyQ