a) Estabilidad nuclear.

b) Explica el origen de la energía liberada en los procesos de fisión y fusión nucleares.

La fisión de un átomo de se produce por captura de un neutrón, siendo los productos principales de este proceso y .

a) Escribe y ajusta la reacción nuclear correspondiente y calcula la energía desprendida por cada átomo que se fisiona.

b) En una determinada central nuclear se liberan mediante fisión . Determina la masa de material fisionable que se consume cada día.

; ; ; ; ;

a) Describe brevemente las interacciones fundamentales de la naturaleza. Compara su alcance e intensidad.

b) El periodo de semidesintegración de un núclido radiactivo de masa atómica 109 u, que emite partículas beta, es de 462.6 días. Una muestra cuya masa inicial era de 100 g, tiene en la actualidad 20 g del núclido original. Calcula la constante de desintegración y la actividad actual de la muestra.

Dato:

a) Representa gráficamente la energía de enlace por nucleón frente al número másico y justifica, a partir de la gráfica, los procesos de fusión y fisión nuclear.

b) En el proceso de desintegración de un núcleo de se emiten, sucesivamente, una partícula alfa y dos partículas beta, dando lugar finalmente a un núcleo de masa 213.995201 u. i) Escribe la reacción nuclear correspondiente; ii) justifica, razonadamente, cuál de los isótopos radiactivos (el o el núcleo que resulta tras los decaimientos) es más estable.

Datos: ; ; ; ;

a) i) Define defecto de masa y energía de enlace de un núcleo. ii) Indica razonadamente cómo están relacionadas entre sí ambas magnitudes.

b) El se puede desintegrar, por absorción de un neutrón, mediante diversos procesos de fisión. Uno de estos procesos consiste en la producción de , dos neutrones y un tercer núcleo . i) Escribe la reacción nuclear correspondiente y determina el número de protones y número total de nucleones del tercer núcleo. ii) Calcula la energía producida por la fisión de un núcleo de uranio en la reacción anterior.

Datos: ; ; ; ; ;

a) Basándote en la gráfica, razona si las siguientes afirmaciones son verdaderas o falsas: i) El es más estable que el . ii) El es más estable que el , por lo que, al producirse la fusión nuclear de dos núcleos de se desprende energía.

b) En algunas estrellas se produce una reacción nuclear en la que el , tras capturar siete partículas alfa, se transforma en . i) Escribe la reacción nuclear descrita y calcula A y Z. ii) Calcula la energía liberada por cada núcleo de silicio.

Datos: ; ; ; ; .

a) Justifica, indicando los principios que aplica, cuál de las reacciones nucleares propuestas no produce los productos mencionados:

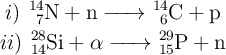
b) i) Determina, indicando los principios aplicados, los valores de c y Z en la siguiente reacción nuclear:

ii) Calcula la energía liberada cuando se fisionan un millón de núcleos de uranio siguiendo la reacción anterior.

Datos: ; ; ; ; ;

a) Explica qué se entiende por defecto de masa y por energía de enlace de un núcleo y cómo están relacionados.

b) Relaciona la energía de enlace por nucleón con la estabilidad nuclear y, ayudándote de una gráfica, explica cómo varía la estabilidad nuclear con el número másico.

Un isótopo de una muestra radiactiva posee un periodo de semidesintegración de 5 730 años.

a) Obtén la vida media y la constante radiactiva del isótopo.

b) Si una muestra tiene átomos radiactivos en el momento inicial, calcula la actividad inicial y el tiempo que debe trascurrir para que dicha actividad se reduzca a la décima parte.

Una muestra contiene inicialmente una masa de 30 mg de . Sabiendo que su período de semidesintegración es de 138.38 días, determina:

a) La vida media del isótopo y la actividad inicial de la muestra.

b) El tiempo que debe transcurrir para que el contenido de de la muestra se reduzca a 5 mg.

Datos: ; .