Ejercicios Resueltos de El movimiento y las fuerzas (4.º de ESO)

Dos automóviles, A y B, se mueven a lo largo de una carretera a la misma dirección. En un momento dado, el automóvil A está a una distancia de 2 km delante de B. Al cabo de 4 minutos, el automóvil B alcanza al A. ¿Cuál de los dos automóviles va a mayor velocidad? ¿Por qué? ¿En cuánto excede la velocidad de uno a la del otro?

En el instante t = 0 una partícula se encuentra a -50 m de un observador. La partícula se mueve con velocidad constante de 10 m/s durante 30 s e inmediatamente frena uniformemente hasta llegar al reposo 20 s después. Suponiendo la dirección del movimiento sobre el eje X positivo, calcula:

a) La aceleración de la partícula durante el frenado.

b) El desplazamiento total de la partícula.

c) La posición de la partícula en el instante que se detiene.

d) La velocidad de la partícula a los 40 s.

e) La rapidez media de la partícula durante los 50 s.

f) La aceleración media durante los 50 s.

Se lanza una piedra hacia arriba desde la parte alta de un edificio de 100 m de altura con una velocidad de 15 m/s y a su regreso pasa cerca del punto de lanzamiento. Calcula:

a) La velocidad de la piedra 1 s y 4 s después de haber sido lanzada.

b) La posición al cabo de 1 s y 4 s.

c) La velocidad cuando esta 6 m por encima del punto de partida.

d) La máxima altura que alcanza y el tiempo en alcanzarla.

Dos trenes pasan en la misma dirección y sentido y a la misma hora por dos estaciones separadas 10 km, con velocidades iguales de . El que va delante frena a razón de mientras que el que va detrás acelera a . Calcula:

a) ¿En qué punto se encontrarán?

b) ¿Cuánto tiempo habrá transcurrido desde su paso por la estación?

c) ¿Qué velocidad tendrá cada tren en ese mismo instante?

Un auto de 600 kg, que circula a 54 km/h, encuentra un obstáculo situado a 70 m de distancia delante de él. El conductor pisa el pedal del freno y consigue detener el coche justo delante del obstáculo. Halla la fuerza que se ejerció sobre el coche durante la frenada.

Un coche de carreras recorre un tramo de una pista variando su velocidad según la gráfica adjunta.

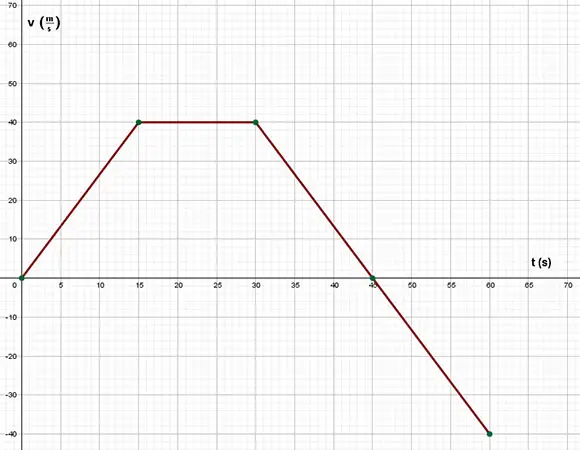
a) Dibuja la gráfica a - t para todo el intervalo.

b) Dibuja la gráfica x - t para los primeros 30 s, sabiendo que .

c) Calcula el desplazamiento total.

Una pelota de tenis cae libremente desde el reposo y se obtienen los siguientes datos para 4.0 s de caída:

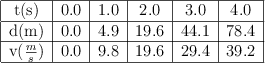
a) Dibuja las gráficas d-t y v-t.

b) Calcula la aceleración para cada intervalo de tiempo.

c) ¿Qué tipo de movimiento es?

Analiza las afirmaciones que se te dan y di cuáles son falsas y cuáles son verdaderas. En caso de ser falsa, explica el porqué:

1) En una gráfica (x, t) de un MRU la recta es creciente a partir del origen.

2) Una recta paralela al eje de las distancias en una gráfica (x, t) representa un movimiento real.

3) En la gráfica (x, t) de un MRU existe una proporcionalidad entre los tiempos empleados y las distancias recorridas.

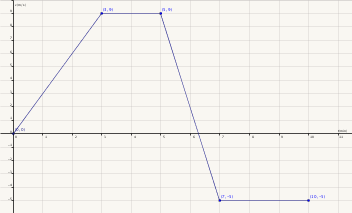
Indica si hay o no movimiento y qué tipo de movimiento es en los distintos tramos de la gráfica s vs t adjunta:

¿Se ha producido cambio de dirección en el movimiento? ¿Cómo lo sabes?

Un joven quiere averiguar la altura a la que se encuentra la ventana de su novia de tal manera que lanza una piedra verticalmente hacia arriba en línea recta desde el suelo que alcanza la altura de la ventana. La piedra llega vuelve al punto de lanzamiento 2.8 s después de que fuera lanzada. Ayuda al joven a averiguar qué altura debe tener la escalera que le permita llegar hasta su amada.