RESUELTO

(6264) ejercicios de RESUELTO

(#8419) Seleccionar

Potenciales de una celda galvánica a distinta temperatura y espontaneidad del proceso (8419)

Se tiene una celda galvánica (pila voltaica) compuesta por dos electrodos: un electrodo de cinc sumergido en una disolución de iones 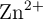$\ce{Zn^{2+}}$ , con una concentración de 1.0 M, y un electrodo de plata sumergido en una disolución de iones 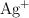$\ce{Ag^+}$ , con una concentración de 1.0 M. Las semirreacciones que ocurren en cada electrodo son las siguientes:

$\left \acute{a}\text{nodo}: \ce{Zn(s) -> Zn^{2+}(aq) + 2e^-} \atop \text{c}{\acute{a}{todo}: \ce{Ag^{+}(aq) + e^- -> Ag(s)} \right \}$

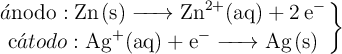
a) Escribe la reacción global de la celda galvánica.

b) Calcula el potencial estándar de la celda (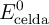 $E^0_{\text{celda}}$ ) utilizando los siguientes potenciales estándar de reducción: 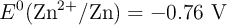$E^0(\ce{Zn^{2+}/Zn}) = -0.76\ \text{V}$ y $E^0(\ce{Ag^+/Ag}) = +0.80\ \text{V}$

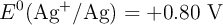
c) Calcula el potencial de la celda a 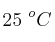$25\ ^oC$ utilizando la ecuación de Nernst, si la concentración de iones 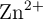$\ce{Zn^{2+}}$ es 0.10 M y la concentración de iones 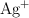$\ce{Ag+}$ es 0.010 M.

d) Determina si la reacción es espontánea en las condiciones dadas.
(#8416) Seleccionar

Energía liberada en la fisión del uranio-235 y reacción de fisión nuclear (8416)

Un núcleo de uranio-235 (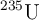 $^{235}\text{U}$ ) experimenta una fisión nuclear y se divide en dos fragmentos, uno de los cuales es kriptón-92 ( 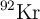$^{92}\text{Kr}$ ) y el otro es bario-141 ( 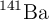$^{141}\text{Ba}$ ). Además, se emiten tres neutrones (3n) en el proceso.

a) Escribe la ecuación nuclear que describe esta reacción de fisión.

b) Calcula la energía liberada en esta reacción, expresada en MeV.

Datos: 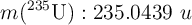$m(^{235}\text{U}): 235.0439\ u$ ; $m(^{92}\text{Kr}): 91.9262\ u$ ; $m(^{141}\text{Ba}): 140.9144\ u$ ; $m_n: 1.0087\ u$ ; $1\ u = 931.5\ MeV\cdot c^{-2}$
(#8417) Seleccionar

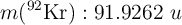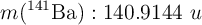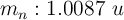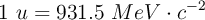
Desintegración alfa, energía liberada y energía cinética de la partícula alfa (8417)

Un núcleo de plutonio-239 (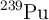 $\ce{^{239}Pu}$ ) experimenta una desintegración alfa y se transforma en uranio-235 $(\ce{^{235}U}$ ).

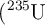a) Escribe la ecuación nuclear que describe esta desintegración alfa.

b) Calcula la energía cinética total liberada en la desintegración, expresada en MeV.

c) Suponiendo que el núcleo de uranio-235 y la partícula alfa comparten la energía liberada, calcula la energía cinética de la partícula alfa.

Datos: 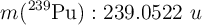$m(\ce{^{239}Pu}): 239.0522\ u$ ; $m(\ce{^{235}U}): 235.0439\ u$ ; $m(\ce{^4He}): 4.0026\ u$ ; $1\ u = 1.66\cdot 10^{-27}\ kg$ ; $c = 3\cdot 10^8\ m\cdot s^{-1}$
(#8415) Seleccionar

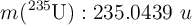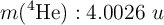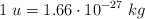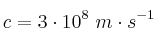
Posición, velocidad, momento lineal y aceleración del centro de masas de un sistema de dos partículas (8415)

Un sistema de dos partículas de masas 2 y 3 kg se mueven en el plano XY. En un instante dado, las posiciones y velocidades de las partículas son:

$\left \vec{r}_1 = (1, 2)\ (m)\ y\ \vec{v}_1 = (3, -1)\ (m\cdot s^{-1}) \atop \vec{r}_2 = (-2, 1)\ (m)\ y\ \vec{v}_2 = (-1, 4)\ (m\cdot s^{-1}) \right \}$

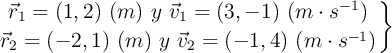
a) Calcula la posición del centro de masas (CM) del sistema.

b) Determina la velocidad del centro de masas.

c) Calcula el momento lineal total del sistema.

d) Determina el momento angular total del sistema respecto al origen.

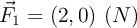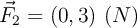e) Si las partículas están sometidas a las fuerzas externas $\vec{F}_1 = (2, 0)\ (N)$ y $\vec{F}_2 = (0, 3)\ (N)$ , calcula la aceleración del centro de masas.
(#8414) Seleccionar

Ecuación de dimensiones del momento de inercia y homogeneidad de algunas fórmulas (8414)

Determina la ecuación de dimensiones del momento de inercia y comprueba la homogeneidad de las siguientes fórmulas físicas:

a) 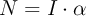$N=I\cdot \alpha$

b) 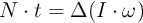$N\c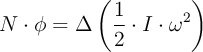dot t = \Delta (I\cdot \omega)$

c) $N\cdot \phi = \Delta \left(\frac{1}{2}\cdot I\cdot \omega^2\right)$

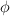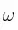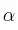donde «N» es el momento del par, «I» es el momento de inercia, «t» es el tiempo y « $\phi$ », « $\omega$ » y « $\alpha$ » son, respectivamente, el ángulo de giro, la velocidad angular y la aceleración angular.