-
Leyes de Newton: resortes elásticos (1374)
Una caja de 2 kg está sobre un plano inclinado de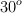 
y sujeta a un resorte cuya elongación es de 3 cm. Si no existe rozamiento entre la caja y el plano:
a) ¿Cuál es la constante recuperadora del resorte?
b) Si desplazamos la caja 5 cm hacia abajo sobre el plano y luego la soltamos, ¿cuál será su aceleración inicial?
-
Ley de Hooke: resortes elásticos (1373)
Un cuerpo de masa m está unido a dos muelles como se ve en la figura. Cada uno de los resortes está estirado con respecto a su posición de equilibrio. Si sus constantes recuperadoras son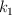 
y 
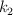respectivamente:
a) Calcula el cociente entre las elongaciones de ambos muelles.
b) Demuestra que si desplazamos el sistema hacia uno de los lados la fuerza recuperadora que aparece es la misma que si el sistema estuviese unido a un único muelle de constante recuperadora 
.
Ley de Hooke
-
Leyes de Newton: resortes elásticos (1372)
Sobre una mesa sin rozamiento se tira con aceleración constante de un objeto de 80 kg mediante un cable que se alarga 0.25 m. Si el bloque estaba en reposo y recorre 5 m en 4 s:
a) ¿Cuál es la constante recuperadora del cable si suponemos que cumple la Ley de Hooke?
b) ¿Cuál sería la elongación del cable si colgásemos verticalmente el objeto y lo dejásemos en reposo?
Dato: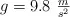 
-
Leyes de Newton: resortes elásticos (1371)
Un resorte tiene una constante recuperadora k = 200 N/m. De él cuelga, inmóvil, un objeto de 5 kg. Hallar el valor numérico de todas las fuerzas que se ejercen sobre el objeto y el alargamiento del resorte respecto a su posición de equilibrio.
Considera que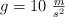 
.
-
Acceso25 UNED: alargamiento de un muelle al colgar una lámpara (1292)
Un muelle tiene una constante recuperadora k = 300 N/m y de él cuelga una lámpara de 6 kg de masa. Calcula el alargamiento del muelle respecto de su posición de reposo.
Ley de Hooke
Ejercicios FyQ