-
Refuerzo: trabajo efectuado sobre una caja (7321)
Una caja de 5.0 kg de masa se acelera desde el reposo mediante una fuerza, con un valor constante de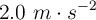 
durante 7 s. Encuentra el trabajo neto realizado sobre la caja.
-
Aceleración, velocidad y posición de un cuerpo a partir de su aceleración angular (7320)
Un cuerpo se mueve sobre una trayectoria circular de radio 5 cm. En el instante t = 0 el cuerpo está en reposo y forma un ángulo de cero grados con el eje positivo de las x. La aceleración angular del cuerpo es:
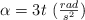
Detemina:
a) El vector posición para cualquier instante de tiempo.
b) La velocidad tangencial en función del tiempo.
c) La aceleración centrípeta en función del tiempo.
d) La aceleración tangencial en función del tiempo.
e) Las aceleraciones tangencial y centrípeta en t = 2.
-
Velocidad y aceleración en un movimiento circular acelerado (7319)
Una partícula se mueve a lo largo de una trayectoria circular de radio 40 cm de tal manera que su posición angular viene dado por:
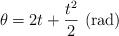
Calcula:
a) La velocidad angular y tangencial para cualquier instante.
b) La aceleración angular y tangencial para cualquier instante.
c) La aceleración normal para t = 2 s.
d) La aceleración total para el instante t = 2 s.
-
Movimiento de despegue de un cohete (7318)
Se lanza un modelo de cohete hacia arriba con una velocidad inicial de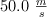 
. Acelera con una aceleración ascendente constante de 
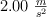hasta que sus motores se detienen a una altitud de 150 m.
a) ¿Qué puedes decir sobre el movimiento del cohete después de que se detienen sus motores?
b) ¿Cuál es la altura máxima alcanzada por el cohete?
c) ¿Cuánto tiempo después del despegue alcanza el cohete su altura máxima?
-
Volumen de una piscina con medidas en el sistema imperial (7308)
Una piscina en forma de paralelepípedo posee las siguientes dimensiones: largo = 54.6 yd, ancho = 82.0 ft y profundidad = 78.7 in. Determina el volumen de agua en litros que se necesitaría para llenar al ras la piscina.
Datos: 1 ft = 0.384 m : 1 yd = 0.914 m ; 1 in = 0.0254 m.
EDICO
Ejercicios FyQ