-
Aceleraciones tangencial y normal a partir del vector de posición (1143)
Una partícula se mueve en el espacio según la función de posición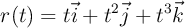 
, en unidades SI. Determina las componentes tangencial y normal de la aceleración en t = 2 s.
-
Velocidad y aceleración de un cubo que gira atado a una cuerda (1089)
Hacemos girar un cubo que contiene agua con una velocidad angular constante de 100 vueltas por minuto. Si la longitud de la cuerda que usamos es de 1.8 m, ¿cuál es la velocidad lineal del cubo? ¿Y su aceleración?
-
Lanzamiento vertical hacia arriba de una pelota desde una ventana (1088)
Un niño lanza hacia arriba una pelota desde el balcón de su casa que está a una altura de 7 m. Sabiendo que la pelota sube durante 0.3 s, determina:
a) La velocidad con la que el niño lanza la pelota hacia arriba.
b) La altura máxima que alcanza la pelota.
c) El tiempo transcurrido hasta que la pelota toca el suelo.
d) La velocidad con la que la pelota llega al suelo.
-
Desplazamiento, distancia y velocidad de un móvil, sabiendo su ecuación de la posición (1090)
El vector de posición de una partícula es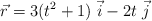 
. Calcula:
a) Los vectores de posición para los instantes 1 y 2 s.
b) El vector desplazamiento y la distancia entre ambas posiciones.
c) La velocidad de la partícula.
d) ¿Qué tipo de movimiento es?
-
Problema física relativista: velocidades relativas de los pasajeros de un tren (993)
Un tren lleva una velocidad constante de 90 km/h. Un viajero camina por el vagón, en el mismo sentido del movimiento del tren, a una velocidad de 0.5 m/s. En el otro extremo otro pasajero camina en sentido contrario a una velocidad de 0.68 m/s. Calcula:
a) La velocidad del primer viajero respecto de un observador situado fuera del tren.
b) La velocidad del segundo viajero respecto del mismo observador.
c) La velocidad del primer viajero con respecto al segundo.
Velocidad
Ejercicios FyQ