-
Velocidad tangencial y mayor valor de la velocidad angular que soporta una moneda que gira
El plato de un tocadiscos gira con una velocidad angular de módulo 4.0 rad/s. Una moneda cuya masa es de 25 g, puesta en el plato, gira con él a una distancia de 15 cm del eje de giro. Si el coeficiente de rozamiento estático entre la moneda y el plato del disco es de 0.80, se pide:
a) Calcula y representa la velocidad tangencial de la moneda.
b) Calcula el valor de la máxima velocidad angular que puede girar el plato del tocadiscos, para que la moneda no salga despedida hacia afuera del mismo.
-
Velocidad lineal y angular de un objeto que gira (5809)
Hallar la velocidad angular y lineal con la que gira un objeto de 120 g si la fuerza a la que está sometido es de 27 N, siendo el radio de giro de 0.89 m.
-
Radio de una pista en un planeta comparado con el radio en la Tierra (5553)
El coeficiente de fricción estática para las llantas de un auto de carreras es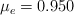 
y el de fricción cinética es 
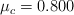. El auto está en una pista circular nivelada de 50.0 m de radio en un planeta donde 
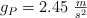. Si el auto es capaz de viajar a la misma rapidez que en la Tierra, donde 
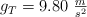, ¿cuántas veces más grande debería ser el radio de la pista en ese planeta con respecto al radio de la pista en la Tierra?
-
Fuerza de rozamiento de un automóvil que traza una curva
La masa de un automóvil es de 1 000 kg traza una curva de radio de 200 m con una velocidad de 108 km/h. Halla la fuerza de rozamiento entre el automóvil y el asfalto.
-
Velocidad de giro del eléctron alrededor del núcleo en el modelo atómico de Bohr (5222)
En el modelo del átomo de Bohr el electrón gira alrededor del núcleo en una órbita circular. Si la fuerza eléctrica que experimenta el electrón debido a la fuerza de atracción con el protón es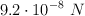 
, el radio del átomo mide 
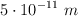y la masa del electrón es 
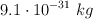, determina la rapidez con la que gira el electrón.
MCU
Ejercicios FyQ