-
Conservación de la energía en un sistema de un bloque que choca contra un resorte (6623)
Un bloque de masa 5 kg se desliza, sobre una superficie horizontal sin rozamiento, con una velocidad de 15 m/s en el momento que choca con un resorte, comprimiéndolo y variando su rapidez a 10 m/s. La constante de elasticidad del resorte es de 500 N/m. Calcula, usando consideraciones energéticas, la deformación del resorte.
-
Teorema de conservación de la energía mecánica aplicado a un resorte que se comprime (6519)
El sistema masa-resorte que se presenta a continuación tiene las siguientes características.
– Masa del bloque: 0.658 kg.
– Velocidad en el punto a): 1.15 m/s.
– Constante de la elasticidad del resorte: 58.0 N/m.
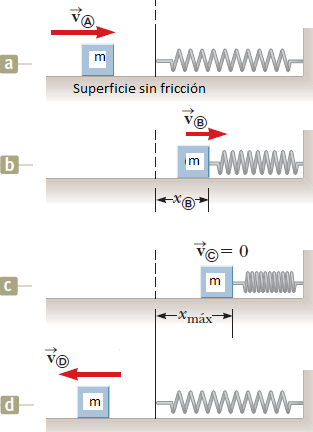
Energía potencial elástica
A partir de la anterior información y basándote en el teorema de conservación de la energía mecánica:
i) Expresa la energía mecánica en cada situación, justificando la respuesta.
ii) Calcula el valor de la comprensión del resorte en c (compresión máxima).
iii) Calcula el valor de la velocidad en d.
iv) Calcula el valor de la velocidad en b asumiendo que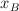 
es la mitad de la compresión máxima del resorte.
-
Fuerza para alargar un muelle y energía potencial que almacena (6489)
Un resorte de k= 2 000 N/m mide 50 cm y al aplicarle una fuerza se alarga hasta llegar a 60 cm. Halla:
a) El valor de la fuerza aplicada.
b) La energía potencial elástica almacenada cuando llega a los 60 cm.
-
Conservación de la energía cuando una esfera choca contra un resorte (6466)
En una práctica, una esfera de masa 1.98 kg que se desliza por una pista horizontal lisa (sin fricción) con una velocidad de 1.26 m/s y choca con un resorte de masa despreciable y constante k = 528 N/m en equilibrio y con uno de sus extremos fijo. A partir de la información anterior, calcula:
a) La distancia que se comprime el resorte.
b) La altura desde la que debería caer la esfera sobre el resorte, si este se coloca verticalmente, para producir la misma compresión del apartado anterior, asumiendo que en ese punto la esfera se detiene.
-
Velocidad de un carro que deforma dos muelles distintos (6319)
Un carro de 5 000 kg de masa lleva una velocidad v y es detenido por dos resortes. Después de que el primer resorte (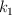
) se comprime 40 cm, entra en acción el segundo resorte (
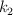) . El carro se detiene 60 cm después de hacer contacto con el primer resorte. Considera que las constantes elásticas de los resortes son: 
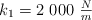y 
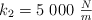. Calcula la velocidad del carro al chocar contra los resortes.
Energía potencial elástica
Ejercicios FyQ