Onda mecánica

(17) ejercicios de Onda mecánica

(#7238) Seleccionar

Tensión de una hebra de seda de araña para una frecuencia fundamental (7238)

Los biólogos piensan que algunas arañas sintonizan hebras de su telaraña para dar una respuesta mejorada en las frecuencias correspondientes a aquellas en las que las presas deseables podrían tener dificultades. La seda de la telaraña de una araña tejedora de orbe tiene un diámetro típico de 20 mm, y la seda de esa araña tiene una densidad de 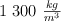$1\ 300\ \textstyle{kg\over m^3}$ . Para tener una frecuencia fundamental a 100 Hz, ¿a que tensión debe ajustar la araña una hebra de seda de 12 cm de largo?
(#6995) Seleccionar

Diferencia de fase entre dos puntos de una onda en función del tiempo (6995)

Considera una onda armónica que se propaga sobre una cuerda con una frecuencia de 600 Hz. ¿Cuál es la diferencia de fase, para un punto de la cuerda dado, entre dos instantes de tiempo separados 0.1 s?
(#6418) Seleccionar

Ecuación de onda de la ola que hace el público de un estadio (6418)

En un estadio el público se hace la ola para celebrar la buena actuación del equipo local. La ola es tan grande que dos espectadores de la misma fila separados por un mínimo de 50 m se mueven igual y lo hacen cada 10 s.

a) Si se ’’modelizase’’ esta ola en el estadio como una onda, ¿de qué tipo de onda se trataría? Calcula su longitud de onda y la pulsación (frecuencia angular).

b) Un espectador se mueve 1.0 m verticalmente cuando se levanta y se sienta al hacer la ola. Escribe la ecuación del movimiento de este espectador considerando que describe un movimiento armónico simple y que en el instante inicial está sentado, es decir, en su posición mínima.

c) Escribe la ecuación de ondas de la ola.
(#5864) Seleccionar

Amplitud, frecuencia, longitud de onda, velocidad y elongación de un onda mecánica (5864)

La ecuación de una onda es:

$y = 0.5\cdot cos\ [2\pi (2t - 4x)]\ (m)$

Determina:

i) Su amplitud, longitud de onda, frecuencia y velocidad de propagación.

¡¡) La elongación de un punto ubicado en la coordenada x = 1 m cuando han transcurrido 0.5 s.
(#5830) Seleccionar

Ecuación de una onda a partir de A, f y v (5830)

Si la onda en una cuerda tensa tiene una amplitud de 0.5 m , una frecuencia de 20 Hz y una velocidad de propagación de 10 m/s, escribe la ecuación de la onda.