-
Aceleración de los bloques en una máquina de Atwood sabiendo el momento de inercia de la polea (7142)
En una máquina de Atwood, dos bloques de masas 12 y 4 kg se desplazan con una aceleración desconocida conectados mediante una cuerda ideal a través de una polea sin fricción de masa 8 kg y radio 0.2 m. Calcula la aceleración de los bloques sabiendo que el momento de inercia de la polea es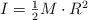 
.
-
Momento angular de una masa que gira en el sentido de las agujas del reloj (7112)
En una instalación existía la posibilidad de hacer movimientos rotacionales. Si uno de los visitantes movió circularmente una masa de 2 kg en el mismo sentido de las manecillas del reloj con una velocidad de 0.5 m/s, siendo la distancia al centro de giro de 60 cm y el ángulo entre el radio y la velocidad de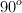 
, determina la cantidad de movimiento angular, su dirección y sentido.
-
Momento angular de un coche que se mueve por una pista circular (6741)
Un coche con una masa de 1 000 kg se mueve con una velocidad de 50 m/s en una pista circular de 100 m de radio. ¿Cuál es la magnitud de su momento angular con respecto al centro de la pista de carreras?
-
Posición, velocidad y momento angular de un sistema de dos partículas distintas (6159)
Las partículas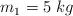 
y 
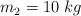tienen movimientos independientes. La partícula 1 se deja libre sobre el plano liso, inclinado un ángulo 
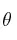, mientras que la partícula 2 se lanza verticalmente hacia abajo desde la altura h con una velocidad inicial de 
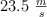. La partícula 2 inicia su movimiento en el instante en que la partícula 1 abandona el plano inclinado. Determina, para t = 2 s después de que la partícula 1 abandona el plano inclinado:
a) La posición del centro de masas del sistema constituido por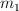 
y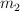 
.
b) La velocidad del centro de masas.
c) El momento angular de cada partícula respecto al origen del sistema de referencia.
Momento angular
-
Posición, velocidad y momentos angular y lineal de un sistema de dos partículas (6158)
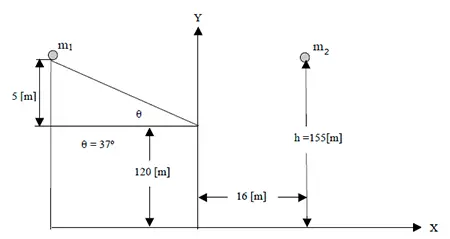
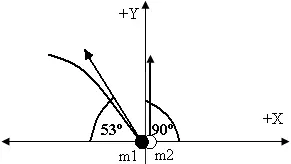
La figura muestra un sistema formado por dos partículas con masas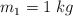 
y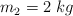 
. Las partículas se lanzan simultáneamente y sus velocidades iniciales son 
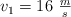y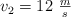 
. Para el instante t = 2 s, determina:
a) La posición del centro de masas del sistema respecto al origen.
b) La velocidad del centro de masas del sistema respecto al origen.
c) El momento angular del sistema respecto al origen.
d) El momento lineal de la partícula 1 respecto al centro de la masas.
Momento angular
Momento angular
Ejercicios FyQ