-
EBAU Andalucía: física (septiembre 2011) - ejercicio A.4 (1974)
La ecuación de una onda en una cuerda es:
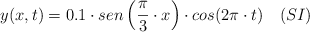
a) Explica las características de la onda y calcula su periodo, longitud de onda y velocidad de propagación.
b) Explica qué tipo de movimiento realizan las partículas de la cuerda y determina la velocidad de una partícula situada en el punto x = 1.5 m, en el instante t = 0.25 s.
-
Selectividad septiembre 2012: ecuación de una onda y velocidad de oscilación (1969)
En una cuerda tensa de 16 m de longitud con sus extremos fijos, se ha generado una onda de ecuación:
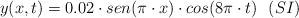
a) Explica de qué tipo de onda se trata y cómo podría producirse. Calcula su longitud de onda y su frecuencia.
b) Calcula la velocidad en función del tiempo de los puntos de la cuerda que se encuentran 4 m y 4.5 m, respectivamente, de uno de los extremos y comenta los resultados.
-
Movimiento ondulatorio: selectividad junio 2012 (1810)
Una onda en una cuerda viene descrita por:
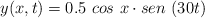(S.I)
a) Explica qué tipo de movimiento describen los puntos de la cuerda y calcula la máxima velocidad del punto situado en x = 3.5 cm.
b) Determina la velocidad de propagación y la amplitud de las ondas cuya superposición daría origen a la onda indicada.
-
Ondas: Frecuencia, longitud de onda y velocidad (1497)
Una antena emite una onda de radio de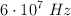 
.
a) Explica las diferencias entre esa onda y una onda sonora de la misma longitud de onda y determine la frecuencia de esta última.
b) La onda de radio penetra en un medio material y su velocidad se reduce a 0.75 c. Determina su frecuencia y su longitud de onda en ese medio.
c =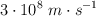 
; v(sonido en el aire) =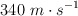 
-
Características de una onda a partir de su función de onda (1496)
La ecuación de una onda armónica es:
y(x,t) = A sen (bt – cx)
a) Indique las características de dicha onda y lo que representa cada uno de los parámetros A, b y c.
b) ¿Cómo cambiarían las características de la onda si el signo negativo fuera positivo?
Velocidad propagación
Ejercicios FyQ