EBAU

(420) ejercicios de EBAU

(#8011) Seleccionar

EBAU Madrid: física (junio 2022) - ejercicio B.3 (8011)

Una carga puntual positiva está situada en el punto (3, 4) m del plano xy. En otro punto del plano se coloca una segunda carga puntual, también positiva y de magnitud el cuádruple de la primera, haciendo que el campo se anule en el origen de coordenadas.

a) Determina la posición de la segunda carga.

b) Si el potencial en el origen de coordenadas vale 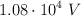$1.08\cdot 10^4\ V$ , encuentra el valor de las cargas.

Dato: 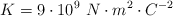$K = 9\cdot 10^9\ N\cdot m^2\cdot C^{-2}$ .
(#8008) Seleccionar

EBAU Madrid: física (junio 2022) - ejercicio B.2 (8008)

Un foco sonoro de potencia P se coloca a una altura h sobre el suelo, como ilustra la figura. El nivel de intensidad sonora vale 60 dB en el punto A, a 100 m de distancia del foco, y alcanza 80 dB en el punto B, en el suelo, en la vertical del foco.

a) Calcula P y h.

b) ¿Cuál sería el nivel de intensidad en el punto B si se agregase sobre él otro foco de igual potencia a una altura de h/2?

Dato: 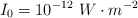$I_0 = 10^{-12}\ W\cdot m^{-2}$ .
(#8006) Seleccionar

EBAU Madrid: física (junio 2022) - ejercicio B.1 (8006)

Marte posee la décima parte de la masa de la Tierra y la mitad de su diámetro.

a) Encuentra la relación entre las velocidades de escape de Marte y de la Tierra desde sus respectivas superficies.

b) Supón que un objeto se lanza verticalmente desde la superficie terrestre, con una velocidad igual a la velocidad de escape de Marte. Si se desprecia el rozamiento, ¿qué altura máxima alcanzaría el objeto?

Dato: 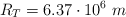$R_T = 6.37\cdot 10^6\ m$ .
(#8005) Seleccionar

EBAU Madrid: física (junio 2022) - ejercicio A.5 (8005)

Una muestra contiene inicialmente una masa de 30 mg de 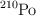$\ce{^210Po}$ . Sabiendo que su período de semidesintegración es de 138.38 días, determina:

a) La vida media del isótopo y la actividad inicial de la muestra.

b) El tiempo que debe transcurrir para que el contenido de 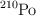$\ce{^210Po}$ de la muestra se reduzca a 5 mg.

Datos: 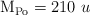$\ce{M_{Po}} = 210\ u$ ; $N_A = 6.02\cdot 10^{23}\ mol^{-1}$ .
(#8002) Seleccionar

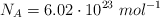EBAU Madrid: física (junio 2022) - ejercicio A.4 (8002)

Dos lentes convergentes idénticas están separadas 16 cm. Cuando un objeto se sitúa a una cierta distancia a la izquierda de la primera lente, se encuentra que cada una de ellas opera con aumento igual a -1.

a) Determina la potencia de las lentes.

b) ¿Cuánto y hacia dónde debe desplazarse la segunda lente para lograr que la imagen del sistema se forme en el infinito?