-
Ampliación: distancia y tiempo que tarda en detenerse una moto por su fricción
Por una pista horizontal se traslada una motocicleta de masa de 150 kg con velocidad inicial de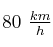 
. Si el coeficiente de rozamiento entre la motocicleta y el asfalto es de 0,2, calcula:
a) El tiempo que tardará en detenerse la motocicleta.
b) La distancia que recorrerá.
-
Trabajo que realiza el motor de un coche para vencer el rozamiento (5850)
Calcula el trabajo que debe hacer el motor de un coche para recorrer un kilómetro con velocidad constante, a pesar del rozamiento, suponiendo que el coche tiene una masa de 1 000 kg y que el coeficiente de rozamiento con el suelo es de 0.3.
-
Distancia total que recorre un automóvil durante la frenada en seco y en mojado (5778)
Un automóvil viaja a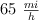 
por un camino recto a nivel cuando el conductor percibe delante una zona de peligro. Después de un tiempo de reacción de 0.5 s aplica los frenos bloqueando las ruedas. El coeficiente de fricción dinámica entre los neumáticos y el camino es 0.6.
a) Determina la distancia total recorrida antes de detenerse, expresada en metros.
b) Si la lluvia disminuye el valor del coeficiente de fricción a 0.4, ¿qué distancia de frenado total recorerrá el automóvil antes de detenerse, expresada en metros?
-
Velocidad de un automóvil sobre el que actúa una fuerza y roza
Un automóvil de 1 250 kg comienza a moverse gracias a una fuerza de 13 800 N sobre una superficie horizontal con coeficiente de fricción de 0.5. ¿Cuál será la velocidad del automóvil a los cinco segundos?
-
Trabajo total sobre una caja que es empujada y que roza con el suelo (5683)
Sobre una caja de 35 kg de masa, Natalia ejerce una fuerza de 300 N paralela a la superficie horizontal y que produce que esta se desplace 4 m. Si el coeficiente de rozamiento cinético entre la caja y la superficie es 0.25, ¿cuál es el trabajo resultante sobre la caja?
Fuerza rozamiento
Ejercicios FyQ