-
Ecuación de la fuerza, periodo, velocidad máxima y energía mecánica de un oscilador armónico (7783)
Una partícula de 10.0 g experimenta un MAS con una amplitud de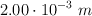 
y una aceleración máxima de magnitud 
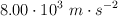. La constante de fase es 
.
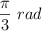a) Escribe una ecuación para encontrar la fuerza sobre la partícula como función del tiempo.
b) ¿Cuál es el periodo del movimiento?
c) ¿Cuál es la máxima rapidez de la partícula?
d) ¿Cuál es la energía mecánica total de este oscilador armónico simple?
-
Periodo de rotación de un péndulo cónico (7677)
Un sistema está constituido por un péndulo cónico que gira con una velocidad angular constante. La cuerda con una longitud L = 20 cm forma un ángulo con la vertical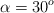 
y está enganchada a una masa m = 5 kg. La masa m se ve afectada por una fuerza vertical F = 20 N. En estas condiciones calcula:
a) El período de rotación del péndulo.
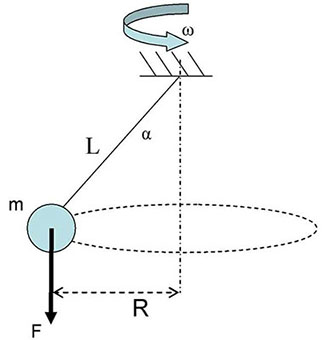
b) Si se mantiene F igual, calcula el valor del nuevo ángulo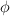 
si la fuerza centrípeta es 50 N.
Periodo
-
Acortamiento de un péndulo para compensar un retraso (6835)
El péndulo de un reloj de péndulo tiene una longitud de 0.994 m. Si el reloj se atrasa 1 minuto por día, ¿cuánto debe acortar el péndulo para hacerlo avanzar a tiempo?
-
Periodo para pequeñas oscilaciones de una masa en un campo unidimensional (6803)
Una partícula de masa «m» se encuentra en un campo potencial unidimensional, donde su energía depende de la coordenada «x» según la ley ![U = U_0 [1 - cos\ (ax)]](local/cache-TeX/78ba7776c6837cd2caf4f8d32ab3d749.png "U = U_0 [1 - cos\ (ax)]")
, en donde «a» y «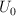
» son constantes. Determina el periodo para pequeñas oscilaciones.
-
Periodo de oscilación y amplitud conociendo la energía de un oscilador
Una partícula de 50 g vibra de forma que, en un punto situado a 4 cm de la posición de equilibrio, la energía cinética y la energía potencial coinciden, y son iguales a 2 J.
a) ¿Cuál es la amplitud del sistema?
b) ¿Cuánto vale el periodo de oscilación?
Periodo
Ejercicios FyQ