-
Ecuación del movimiento y distancia a un punto en función del tiempo de un oscilador armónico
Una partícula describe un movimiento armónico simple sobre el eje X. El centro de oscilación se halla en el eje de origen de coordenadas, la amplitud es 2 m y el periodo 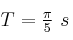 . La posición en el instante inicial es (x = 2 m, y = 0).
. La posición en el instante inicial es (x = 2 m, y = 0).
a) Halla la ecuación del movimiento (posición en función del tiempo).
b) Halla la distancia de la partícula al punto (x = 0, y = 2 m) en función del tiempo.
-
MAS: Frecuencia, desfase y periodo 0001
Una partícula describe un movimiento armónico simple según la siguiente ecuación: x(t) = 0,3 sen (2t + 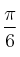 ), en la que la distancia se mide en metros y el tiempo en segundos. Determínese la frecuencia, el periodo, la frecuencia angular y el desfase inicial del movimiento. Calcule la posición de la partícula para t = 1 s. Calcule, por último, la posición, la velocidad y la aceleración de la partícula en el instante inicial.
), en la que la distancia se mide en metros y el tiempo en segundos. Determínese la frecuencia, el periodo, la frecuencia angular y el desfase inicial del movimiento. Calcule la posición de la partícula para t = 1 s. Calcule, por último, la posición, la velocidad y la aceleración de la partícula en el instante inicial.
-
Problema M.A.S 0001
El movimiento de una partícula viene dado por la ecuación 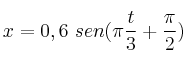 en unidades SI. Calcula:
en unidades SI. Calcula:
a) Las constantes del movimiento.
b) ¿Cuál es la frecuencia de la vibración?
c) Calcula la posición de la partícula para los instantes 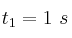 y
y 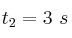 .
.
 Desfase
Desfase