-
Características de una onda creada en el centro de una piscina circular (8216)
En el centro de una piscina circular de 6 m de radio se produce una perturbación que origina un movimiento ondulatorio en la superficie del agua. La longitud de onda es de 0.50 m y tarda 12 s en llegar a la orilla. Calcula la frecuencia del movimiento ondulatorio. ¿Cuál es la amplitud del mismo si al cabo de 0.25 s la elongación en el origen es de 4 cm? Determina la elongación en el instante t = 12 s en un punto situado a 6 m del foco emisor.
-
Magnitudes características de una onda y velocidad y aceleración de un punto (8190)
La ecuación de una onda, en unidades del S.I., que se propaga por una cuerda es:
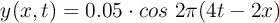
a) Determina las magnitudes características de la onda (amplitud, frecuencia angular, número de onda, longitud de onda, frecuencia, periodo, velocidad de propagación).
b) Deduce las expresiones generales de la velocidad y aceleración transversal de un elemento de la cuerda y sus valores máximos.
c) Determina los valores de la elongación, velocidad y aceleración de un punto situado a 1 m del origen en el instante t = 3 s.
-
Desplazamiento de las moléculas y amplitud de presión en una onda sonora (7769)
a) Calcula el desplazamiento máximo de las moléculas de aire cuando una onda de sonido de 210 Hz tiene alcanza la intensidad sonora del umbral del dolor, es decir, los 120 dB.
b) ¿Cuál es la amplitud de presión de la onda?
-
Amplitud de la onda en una manguera tensada (7161)
Una manguera de hule, con densidad lineal de 0.05 kg/m, se mantiene a una tensión de 30 N. Un extremo de la manguera se fija a un dispositivo que evita la reflexión de cualquier energía hacia el otro extremo y se le hace vibrar con una frecuencia de 4 Hz. ¿Cuál debería ser la amplitud de dicha vibración para que la energía se transmita con una potencia de 12 W?
-
Movimiento ondulatorio: selectividad junio 2012 (1810)
Una onda en una cuerda viene descrita por:
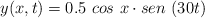 (S.I)
(S.I)
a) Explica qué tipo de movimiento describen los puntos de la cuerda y calcula la máxima velocidad del punto situado en x = 3.5 cm.
b) Determina la velocidad de propagación y la amplitud de las ondas cuya superposición daría origen a la onda indicada.
 Amplitud
Amplitud