-
EBAU Andalucía: física (junio 2024) - ejercicio A.2 (8288)
a) i) Deduce razonadamente la expresión de la velocidad de escape de un cuerpo desde la superficie de un planeta. ii) La masa y el radio de la Tierra son 81 y 3.67 veces la masa y el radio de la Luna, respectivamente. ¿Qué relación existe entre las velocidades de escape desde las superficies de la Tierra y la Luna? Razona tu respuesta.
b) Se desea poner alrededor de Júpiter un satélite artificial en órbita circular estacionaria (igual periodo que el planeta). Un día en Júpiter es 0.41 veces el día terrestre y la masa de Júpiter es 318 veces la de la Tierra. Determina: i) el radio orbital alrededor de Júpiter; ii) la relación que existe entre los radios orbitales de dos satélites que orbitan estacionariamente alrededor de la Tierra y de Júpiter.
; 
; 
-
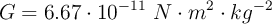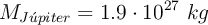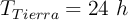
EBAU Madrid: física (junio 2022) - ejercicio B.1 (8006)
Marte posee la décima parte de la masa de la Tierra y la mitad de su diámetro.
a) Encuentra la relación entre las velocidades de escape de Marte y de la Tierra desde sus respectivas superficies.
b) Supón que un objeto se lanza verticalmente desde la superficie terrestre, con una velocidad igual a la velocidad de escape de Marte. Si se desprecia el rozamiento, ¿qué altura máxima alcanzaría el objeto?
Dato: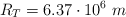 
.
-
Velocidad de un proyectil para que ascienda una altura y para que escape de un planeta (6953)
Desde la superficie de un planeta esférico sin atmósfera, de masa M y de radio R, se lanza verticalmente un proyectil que llega a alcanzar una altura máxima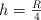 
antes de caer a su superficie. ¿Con qué velocidad inicial 
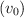se ha lanzado el proyectil? ¿Con qué velocidad inicial mínima 
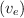habrá que lanzarlo para que escape de la atracción gravitatoria del planeta y no vuelva a caer?
-
Velocidad de escape en la Tierra (5674)
¿Cuál es la velocidad de escape de la Tierra?
Datos: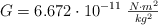 
; 
; 
; 
-
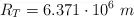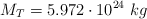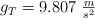
Examen de Fundamentos de Física I: Gravedad y velocidad de escape (2246)
El mecanismo que sigue un saltador de altura al realizar un salto consiste en comunicar a su cuerpo una energía inicial que se convierte en energía potencial al alcanzar su altura máxima. Supongamos que tenemos dos asteroides; Rocón y Gordón, que tienen los dos la misma densidad de masa que la Tierra,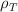 
.
a) Suponiendo que tenemos un saltador de altura capaz de saltar dos metros en la Tierra, calcula el radio que debe tener el asteroide Rocón para que ese saltador de altura pueda escapar del asteroide de un salto.
b) Si sabemos que el asteroide Gordón tiene un radio de 8 km, ¿qué altura puede alcanzar nuestro saltador en Gordón?
c) Si otro saltador más fuerte que está en Rocón puede impulsarse a una velocidad doble de la velocidad de escape de Rocón, ¿qué velocidad tendrá cuando se encuentre muy lejos del asteroide?
(Datos: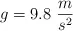 
; 
; 
)
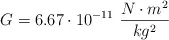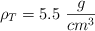Velocidad escape
Ejercicios FyQ