Ley de Hooke

(44) ejercicios de Ley de Hooke

(#8220) Seleccionar

Constante de recuperación de un muelle y relación entre masa y deformación (8220)

Encuentras un muelle en la calle y quieres saber cuál es la constante de recuperación del muelle para saber si puedes usarlo para construir un juguete. Para ello, cuelgas distintas masas del muelle y mides el alargamiento que experimenta. Los datos que obtienes están registrados en la siguiente tabla:

$\begin{tabular}{| c | c |} \hline Masa (kg) & Alargamiento (cm) \\\hline 0.5 & 0.8 \\\hline 1.0 & 1.6 \\\hline 1.5 & 2.4 \\\hline 2.0 & 3.2 \\\hline 2.5 & 4.0 \\\hline \end{tabular}$

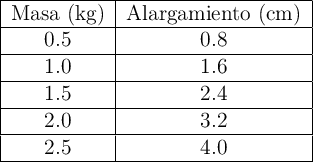
a) Representa los valores de la tabla en una gráfica.

b) ¿Cuál es la constante de recuperación del muelle?

c) ¿Qué masa necesitarías colgar del muelle para que se alargara exactamente 2.0 cm?

d) ¿Qué valor estimas que se estiraría el muelle al colgarle una masa de 3.0 kg?

e) ¿Qué ley física se cumple? Expresála con palabras.
(#7700) Seleccionar

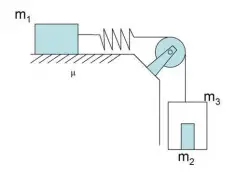
Dinámica de un sistema de cuerpos unidos por un muelle y una cuerda (7700)

El siguiente sistema está compuesto por tres masas de igual valor 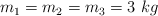$m_1 = m_2 = m_3 = 3\ kg$ . La constante de recuperación del muelle es 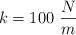$k = 100\ \textsyle{N\over m}$ . El cuerpo 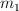$m _1$ tiene coeficientes de fricción con el suelo 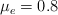$\mu_e = 0.8$ y $\mu_c = 0.2$ .

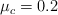Ley de Hooke

a) Si el sistema se encuentra en reposo: calcula la fuerza de fricción y la longitud que se estira el muelle.

b) Si el sistema se encuentra en movimiento: calcula la fuerza de contacto entre 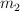$m _2$ y $m _3$ .
(#7669) Seleccionar

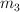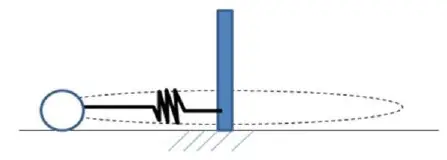
Ampliación: dinámica del movimiento circular y ley de Hooke (7669)

Un muelle varía su longitud natural de 1.5 m (longitud en reposo) por la acción de la rotación de una masa 1 kg pegada a ella. Supón que no hay fricción, que la velocidad angular es 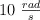$10\ \textstyle{rad\over s}$ y que la constante del muelle tiene un valor de $1\ 500\ \textstyle{N\over m}$ .

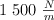Ley de Hooke

a) Calcula la elongación (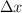 $\Delta x$ ) que sufre el muelle. ¿Cuál será la nueva longitud del muelle?

b) Calcula la fuerza centrípeta, la aceleración normal y la fuerza normal.

c) Calcula el valor de una fuerza F en la dirección radial si se pretende disminuir la velocidad angular en un 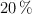$20 \%$ y se observa que la elongación del muelle es la mitad que en el primer apartado.
(#7627) Seleccionar

Aplicación de la conservación de la energía mecánica a un ascensor que cae (7627)

Un ascensor tiene una masa de 1 250 kg y las personas que van en su interior de 350 kg. El foso mide 120 cm y el muelle de emergencia 100 cm, pudiéndose comprimir como máximo 40 cm. Al pasar por el 5.º piso, a una altura de 19 m, y mientras desciende con una velocidad constante de 2 m/s, se rompe el cable que sujeta el ascensor y se acciona el sistema de frenado hidráulico sobre los rieles de la cabina, provocando una fuerza de rozamiento de 15 000 N.

a) Calcula la constante elástica que debe tener el muelle para que no llegue a comprimirse totalmente.

b) ¿Cambiaría en algo si estuviese subiendo? ¿Y si no hubiese fuerza de rozamiento?

c) Si por seguridad la constante elástica del muelle se aumenta en un 20%, ¿Cuánto se comprimirá el muelle?
(#7554) Seleccionar

Constante elástica de los amortiguadores de un coche (7554)

Cuando un coche esta cargado con 25 kg, su altura es de 25 cm. Si lo cargamos con 75 kg, su altura desciende a 20 cm. ¿Cuál es la constante elástica de los amortiguadores y cuál es la altura del coche cuando no está cargado?