-
Masa de un joven para que el balancín permanezca en equilibrio (7775)
Un joven de 100 lb de masa se sienta en el extremo izquierdo de un sube y baja de 8 ft de largo apoyado en el centro. Si otro joven se sienta a 1 pie del extremo derecho, ¿cuál debe ser su masa para que el sistema esté en equilibrio? ¿Cuál es la fuerza ejercida por el soporte?
-
Ecuación que permite calcular la fuerza necesaria para que una escalera esté en equilibrio sobre la pared (7574)
Una escalera de peso W y longitud L se apoya sobre una pared sin rozamiento. Sobre la escalera se encuentra una persona de peso P, a una distancia S del pie de la escalera, medida a lo largo de esta. El pie de la escalera se encuentra a una distancia D de la esquina inferior de la pared. Determina una expresión para la fuerza que la pared ejerce sobre la escalera, considerando que el sistema se encuentra en equilibrio estático.
-
Peso máximo de un bloque para que el sistema permanezca en equilibrio (7311)
El bloque B en la pesa 711 N. El coeficiente de fricción estática entre el bloque B y la mesa es 0.25 y el ángulo es de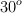 
. Suponiendo que la cuerda entre B y el nudo es horizontal, ¿cuál es el peso máximo del bloque A para el que el sistema estará en equilibrio?
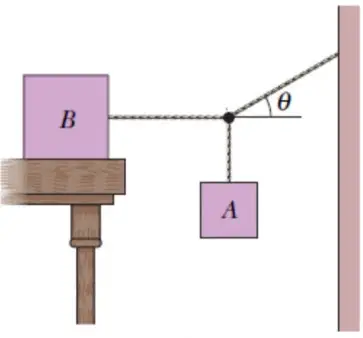
Equilibrio
-
Tensión en el cable y fuerza sobre el gozne de un sistema en equilibrio estático (7310)
En la siguiente figura, la viga uniforme de 725 N de peso está sujeta a un pasador en el punto A:
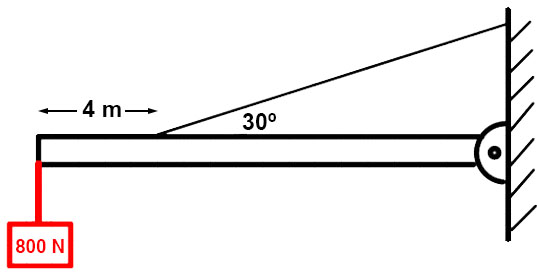
Equilibrio
a) Determina la tensión en la cuerda.
b) Calcula las componentes de la fuerza que ejerce el apoyo sobre la viga.
-
Tensión del cable en una situación de equilibrio (6793)
En la figura que se muestra, determina la tension en el cable, si la barra es homogénea y de masa insignificante.
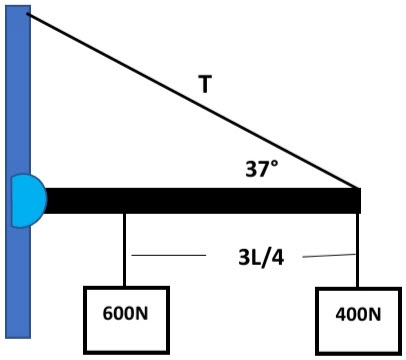
Equilibrio
Equilibrio
Ejercicios FyQ