-
Ecuación que permite calcular la fuerza necesaria para que una escalera esté en equilibrio sobre la pared (7574)
Una escalera de peso W y longitud L se apoya sobre una pared sin rozamiento. Sobre la escalera se encuentra una persona de peso P, a una distancia S del pie de la escalera, medida a lo largo de esta. El pie de la escalera se encuentra a una distancia D de la esquina inferior de la pared. Determina una expresión para la fuerza que la pared ejerce sobre la escalera, considerando que el sistema se encuentra en equilibrio estático.
-
Tensión en el cable y fuerza sobre el gozne de un sistema en equilibrio estático (7310)
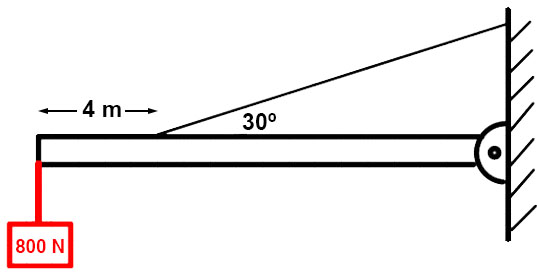
En la siguiente figura, la viga uniforme de 725 N de peso está sujeta a un pasador en el punto A:
Momento
a) Determina la tensión en la cuerda.
b) Calcula las componentes de la fuerza que ejerce el apoyo sobre la viga.
-
Momento de una fuerza aplicada sobre una pieza mecánica (6889)
Una fuerza que actúa sobre una pieza mecánica es 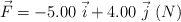 . El vector del origen al punto de aplicación de la fuerza es
. El vector del origen al punto de aplicación de la fuerza es 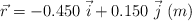 :
:
a) Realiza un esquema que muestre los vectores 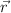 ,
, 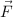 y el origen de coordenadas.
y el origen de coordenadas.
b) Usa la regla de la mano derecha para determinar la dirección del vector resultante.
c) Calcula el vector del momento producido por la fuerza y verifica que su dirección sea la misma que indicaste en el apartado anterior.
-
Centro de masas de una lámina de aluminio y hierro (5688)
Se tiene una lámina metálica de dimensiones 22 cm x 13 cm x 2.8 cm. La mitad de la lámina está compuesta por aluminio (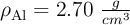 ) y la otra mitad por hierro (
) y la otra mitad por hierro (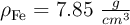 ). ¿Dónde se situará el centro de masas de la lámina?
). ¿Dónde se situará el centro de masas de la lámina?
-
Palancas: masa máxima que podemos levantar al aplicar una fuerza (5438)
Calcula la masa máxima, en kilogramos, que podemos levantar si aplicamos 500 N de fuerza sobre un extremo de una palanca de 5 m de longitud, si el punto de apoyo se encuentra a 3 m de nosotros. Considera que 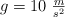 .
.
 Momento
Momento