-
Constante de velocidad y tiempo de vida media para una reacción de primer grado (8459)
Se ha estudiado la descomposición del compuesto «A» en productos a una temperatura constante de 298 K. La reacción es de primer orden respecto a «A». A continuación, se proporcionan los datos experimentales de la concentración de «[A]» en función del tiempo:
![\begin{tabular}{| c | c |} \hline tiempo\ (s) & [A]\ (\text{mol}\cdot L^{-1}) \\\hline 0&1.000\\\hline 50&0.607\\\hline 100&0.368\\\hline 200&0.135\\\hline 300&0.050\\\hline \end{tabular}](local/cache-TeX/3d221adca24eb6004ced5083ef82c57a.png "\begin{tabular}{| c | c |} \hline tiempo\ (s) & [A]\ (\text{mol}\cdot L^{-1}) \\\hline 0&1.000\\\hline 50&0.607\\\hline 100&0.368\\\hline 200&0.135\\\hline 300&0.050\\\hline \end{tabular}")
Determina la constante de velocidad de la reacción «k», utilizando la regresión lineal como método gráfico, y el tiempo de vida media de la reacción.
-
Análisis dimensional de la fuerza «centrígufa» en un sistema no inercial (8458)
En mecánica, la fuerza «centrífuga» en un sistema rotatorio no inercial se expresa como:
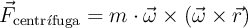
donde: «m» es la masa de la partícula (en kg), «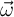
» es la velocidad angular y «
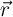» es el vector de posición, todas la magnitudes expresadas en unidades SI.
a) Determina las dimensiones de la fuerza «centrífuga» y verifica que coincidan con las de una fuerza.
b) Si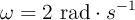 
y r = 0.5 m, calcula el módulo de la fuerza «centrífuga» para una masa de 3 kg.
-
Velocidad y aceleración de un móvil en función del tiempo (8457)
Un móvil describe una trayectoria en el plano XY dada por el vector de posición, expresado en unidades SI:
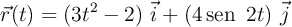
a) Determina los vectores velocidad y aceleración en función del tiempo.
b) Calcula los vectores velocidad y aceleración en el instante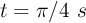 
.
c) Halla el módulo de la velocidad y de la aceleración en .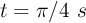
-
Constante de desintegración y actividad radiactiva de la desintegración alfa del radio (8455)
Un núcleo de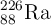 
(radio-226) experimenta desintegración 
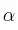con una vida media 
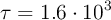años, transformándose en 
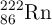(radón-222).
a) Escribe la reacción nuclear correspondiente a este proceso.
b) Calcula la constante de desintegración (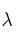
), expresada en 
.
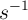c) Determina la actividad inicial de una muestra de 1.00 g de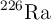 
.
d) ¿Cuánto tiempo tardará la muestra en reducir su actividad al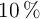 
del valor inicial, expresado en años?
Datos: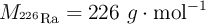 
; 
.
-
Trabajo y potencia de una fuerza variable que provoca un desplazamiento (8450)
Un bloque de 5 kg de masa se desplaza sobre una superficie horizontal bajo la acción de una fuerza variable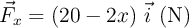 
, donde «x» es la posición en metros. El coeficiente de rozamiento cinético entre el bloque y la superficie es 
.
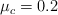a) Calcula el trabajo realizado por la fuerza cuando el bloque se mueve desde x = 0 hasta x = 10 m.
b) Determina el trabajo realizado por la fuerza de rozamiento en el mismo desplazamiento.
c) Si el bloque parte del reposo en x = 0, ¿cuál será su velocidad en x = 10 m?
d) ¿Qué potencia media desarrolla la fuerza durante este proceso?
Dato: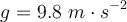 
RESUELTO
Ejercicios FyQ