Ejercicios Resueltos de El movimiento y las fuerzas (4.º de ESO)

Dos alumnos muy enojados entre sí están en reposo uno frente al otro, distanciados 24 metros. En un instante dado, ambos parten para encontrarse. Suponiendo que sus aceleraciones son constantes y de y , respectivamente. Determina:

a) En qué punto del camino se encuentran.

b) Qué velocidad tiene cada uno en ese instante.

La velocidad de un río es de 5 m/s y la anchura del mismo de 80 m. De una orilla y perpendicularmente a la misma, sale una barca con velocidad respeto a tierra de 2 m/s. Al mismo tiempo por el centro del río y a contracorriente, sale otra barca desde un punto situado a 500 m aguas abajo del primero. El cruce de ambos barcos tiene lugar en el punto medio del río a igual distancia de ambas orillas. Calcular el tiempo que tardan en encontrarse, el espacio recorrido por la segunda barca y la velocidad de esta respecto al agua.

Dos proyectiles A y B se disparan simultáneamente hacia arriba con velocidades de 20 y 30 m/s. Si A se encuentra 60 m sobre B, que está en el suelo, determina:

a) El tiempo que pasará hasta que ambos proyectiles estén a la misma altura.

b) La altura, respecto del suelo, a la que se encontrarán ambos en ese instante.

Programamos un coche teledirigido para que siga un movimiento rectilíneo que siga la ecuación s = 3t - 3 (S.I). Un obstáculo está situado a 12 m de la posición inicial del coche. ¿Qué tiempo tardará el coche en llegar hasta él? ¿Cuál será la posición del coche a los 2 s de iniciado el movimiento?

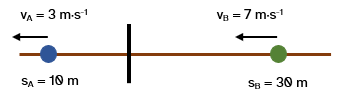
Escribe las ecuaciones de la posición de cada uno de los objetos que se representan en la figura y determina, gráfica y analíticamente, en qué posición se encuentran, con respecto al origen.

Un automóvil parte del reposo y se mueve con una aceleración constante durante 6 s. ¿Cómo podrías calcular la velocidad inicial y final y el desplazamiento inicial y final del automóvil?

Un vehículo que se desplaza a acelera durante un tiempo de 8 s llegando a una velocidad de :

a) ¿Cuál es el espacio que recorrió durante ese tiempo, expresada en metros?

b) ¿Qué aceleración, en , tiene dicho vehículo?

Un móvil parte del reposo con una aceleración de . Calcula el espacio recorrido en el tercer segundo.

Un colectivo circula a y comienza a frenar, durante 6 s, llegando a reducir su velocidad a . Calcula:

a) ¿Cuál fue el espacio que recorrió mientras frenaba, expresado en metros?

b) ¿Cuál fue su desaceleración, expresada en ?

c) ¿En qué tiempo llegaría a frenar del todo manteniendo esa desaceleración?

Juana se encuentra viajando por un camino recto en su automóvil, de regreso de casa de su amiga en el campo, a una velocidad constante de 60 km/h. Luego de 2 minutos de la partida de Juana, Marta, quien reside en dicho campo, observa que su amiga se ha dejado el celular sobre la mesa por lo que decide tomar su motocicleta y alcanzar a su amiga, para poder devolver dicho aparato.

a) ¿A qué distancia de la casa del campo se encuentra Juana en el momento que Marta sale a su alcance?

b) A 5 km se encuentra la carretera principal, donde, debido al tránsito, Marta sabe que será más difícil ubicar a su amiga ¿Qué aceleración deberá implementar Marta para alcanzar a su amiga antes de que esta llegue a la carretera principal y le sea más difícil encontrarla?

c) Realiza las gráficas de a(t), v(t) y x(t) para cada uno de los vehículos.