El movimiento de una partícula viene dado por las ecuaciones , , en donde x e y se miden en metros y t, en segundos. Calcula:

a) La posición de la partícula en cualquier instante.

b) La posición en los instantes t = 0 y t = 2.

c) ¿Dónde se encuentra la partícula a los 5 segundos?

d) ¿A qué distancia del origen del sistema de referencia se encuentra la partícula en ese instante?

La altura de un helicóptero sobre el suelo está dada por la ecuación , donde «h» está en metros y «t» en segundos. Después de 2 s, el helicóptero libera una pequeña valija de correo, ¿cuánto tiempo tardará en tocar esa valija el suelo?

En un edificio de 70 pisos (1.8 metros de altura por piso), tres estudiantes lanzan al mismo tiempo, en pisos diferentes, objetos diferentes entre sí. El primer estudiante se ubica en el piso trece y desde allí lanza verticalmente hacia arriba un objeto con una velocidad de 180 km/h; el segundo estudiante se ubica en el piso dieciocho y desde allí lanza verticalmente hacia arriba su objeto con una velocidad de 100 km/h y el tercer estudiante se ubica en el piso veintitrés y desde allí lanza verticalmente su objeto hacia arriba con una velocidad de 80 km/h.

a) ¿En qué piso del edificio pasan juntos los objetos lanzados desde el piso dieciocho y el piso trece?

b) ¿En qué piso del edificio pasan juntos los objetos lanzados desde el piso veintitrés y el piso dieciocho?

c) ¿En qué piso del edificio pasan juntos los objetos lanzados desde el piso veintitrés y el piso trece?

d) ¿Qué velocidad llevan los objetos lanzados del piso dieciocho y el piso trece, cuando el uno pasa junto al otro?

e) ¿Qué velocidad llevan los objetos lanzados del piso veintitrés y el piso dieciocho, cuando el uno pasa junto al otro?

f) ¿Qué velocidad llevan los objetos lanzados del piso veintitrés y el piso trece, cuando el uno pasa junto al otro?

g) ¿En qué orden llegan los objetos al suelo?

h) ¿Con qué velocidad impacta cada objeto contra el suelo?

i) ¿Cuál es la altura máxima alcanzada por cada objeto con respecto a su punto de lanzamiento?

En una feria, se gana una jirafa de peluche lanzando una moneda a un platito, el cual está sobre una repisa más arriba del punto en que la moneda sale de la mano y a una distancia horizontal de 2.1 m desde ese punto (ver figura). Si se lanza la moneda con velocidad de , y un ángulo de sobre la horizontal, la moneda caerá en el platito. Ignora la resistencia del aire y responde:

a) ¿A qué altura está la repisa sobre el punto donde se lanza la moneda?

b) ¿Cuál es la altura máxima alcanzada por la moneda?

c) ¿Cuál es la velocidad de la moneda un instante antes de tocar el plato?

El vector de posición de un móvil viene dado por la expresión , en unidades SI. Determina:

a) La posición del móvil para t = 1 s y para t = 3 s.

b) El vector desplazamiento entre estos instantes y su módulo.

c) La ecuación de la trayectoria.

Una nadadora intenta cruzar la piscina. Las ecuaciones paramétricas que determinan su trayectoria en unidades SI son:

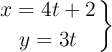
Determina:

a) El vector posición en t = 0 y t = 5 s.

b) La distancia al origen para t = 5 s.

c) El vector desplazamiento entre los instantes t = 0 y t = 5 s.

d) La velocidad media entre t = 0 y t = 5 s.

Un coche deportivo recorre una pista circular de 400 m de diámetro con velocidad constante de 180 km/h. Determinar:

a) La frecuencia del movimiento en rpm.

b) El período.

c) El tiempo necesario para que el coche recorra 800 m.

d) La aceleración centrípeta que experimenta el piloto en términos de la gravedad.

Una piedra se deja caer sobre un pozo con agua y a los dos segundos se escucha el impacto de la piedra sobre el agua. ¿Cuál es la profundidad del pozo?

Un proyectil es disparado por un cañón con una velocidad de 120 m/s y un ángulo de con la horizontal. Encuentra:
a) Su posición (coordenadas xy) después de 7 s.
b) Su velocidad y dirección después de 10 s.
c) El valor máximo que puede alcanzar durante su trayectoria.
d) El tiempo que está en el aire.
e) El alcance del proyectil, asumiendo que el piso está nivelado.

Desde la azotea de un edificio de 50 pisos (2 metros de altura por piso), se lanza un proyectil con un ángulo de inclinación de con respecto a la horizontal, con el propósito de impactar en la azotea de un edificio de 23 pisos (2 metros de altura por piso), que se encuentra alejado 500 metros y, para que el proyectil no sea detectado por las defensas del edificio, este debe durar en el aire 13.5 segundos como máximo.

Con la información suministrada y efectuando los procesos matemáticos correspondientes, responde a las preguntas siguientes:

a) ¿Cuál es la velocidad de lanzamiento del proyectil para lograr el objetivo?

b) ¿Cuál es la velocidad con la que impacta el proyectil contra la azotea del edificio de 23 pisos?

c) ¿Cuál es la altura máxima alcanzada por el proyectil desde su lanzamiento?

d) ¿Cuál es el ángulo de impacto del proyectil con respecto a la vertical?

e) ¿Cuál es el tiempo que tarda el proyectil en lograr su altura máxima?

f) ¿Cuál es la velocidad con la que el proyectil efectúa su trayectoria horizontal?

g) ¿Cuál es el tiempo que tarda el proyectil en caer desde su punto de máxima altura hasta lograr el objetivo?