-
Movimiento vibratorio en una cuerda tensa (7779)
Un extremo de una cuerda tensa horizontal de 3 m de longitud está sometida a un movimiento vibratorio armónico simple. En el instante t = 4 s la elongación de ese punto es de 2 cm. Se comprueba que la onda tarda 0.9 s en llegar de un extremo a otro de la cuerda y que la longitud de onda es de 1 m. Calcula:
a) La amplitud del movimiento ondulatorio.
b) La velocidad de vibración en el punto medio de la cuerda para t = 1 s.
-
Periodo de oscilación y amplitud conociendo la energía de un oscilador
Una partícula de 50 g vibra de forma que, en un punto situado a 4 cm de la posición de equilibrio, la energía cinética y la energía potencial coinciden, y son iguales a 2 J.
a) ¿Cuál es la amplitud del sistema?
b) ¿Cuánto vale el periodo de oscilación?
-
Velocidad, amplitud y frecuencia de un oscilador armónico a partir de su ecuación de la posición
La ecuación del movimiento de una partícula (en unidades SI) viene dada por:
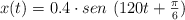
a) ¿Cuál es la ecuación de la velocidad?
b) ¿Cuáles son las condiciones iniciales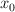 
y 
?
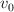c) ¿Cuáles son la amplitud y la frecuencia del movimiento?
-
Aceleración de un MAS para un valor de amplitud dado
La posición, en cm, de un MAS viene dada por la ecuación: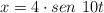 
, donde t es el tiempo en s. Calcula la aceleración en el instante en que la amplitud es 3 cm.
-
Estudio de la posición del péndulo de un reloj y su periodo
El péndulo de un reloj se mueve periódicamente, separándose s (cm) de la vertical. La ecuación que describe el movimiento es:
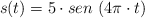
a) Decide a qué distancia de la vertical y de que lado de la misma estará el péndulo a los 2 s.
b) ¿Qué distancia máxima alcanza?
c) ¿En qué instante alcanza la distancia máxima?
d) ¿Cuál es su periodo?
Amplitud
Ejercicios FyQ