-
Conservación de la energía en un sistema con tramos sin y con rozamiento (6096)
Un cuerpo de 1.5 kg se encuentra incicialmente comprimiendo 0.3 m un resorte de constante elástica de 800 N/m. Al liberar el resorte se desliza, sin rozamiento, por un riel y alcanza un tramo circular:
a) Sabiendo que la velocidad del cuerpo en el punto más alto del círculo es de 2.0 m/s, calcula el radio del tramo circular.
b) Al salir del tramo circular llega a un tramo rugoso de 3 m con coefciente de rozamiento de 0.25. ¿Cuál es la velocidad del cuerpo al atravesar ese tramo?
-
Compresión de un resorte para que la altura de un objeto sea el doble (6050)
Un resorte se comprime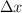 
para lanzar verticalmente hacia arriba un objeto que alcanza una altura h. Para duplicar la altura alcanzada la compresión del resorte debe ser de:
a)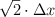 
.
b)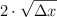 
.
c)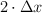 
.
d) Ninguna es correcta.
-
Energía potencial de un resorte y trabajo neto realizado (6041)
Un niño construye un juguete con un resorte que mide 20 cm de longitud (cuando sobre no se aplica fuerzas externas) y una tapa de 20 cm de diámetro, como se muestra en la figura.
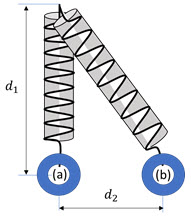
Energía potencial elástica
Inicialmente el niño estira el resorte verticalmente 93.8 cm (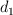
) y luego mueve el juguete horizontalmente 76.5 cm (
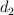), es decir de la posición (a) a la posición (b). Si la constante de elasticidad del resorte es 25.1 N/m, calcula:
a) La energía potencial elástica en la posición (a) y en la posición (b).
b) El trabajo neto realizado.
-
Sistema disparado verticalmente por un resorte (5974)
Un resorte liviano de constante elástica k = 200 N/m, está comprimido x = 0.20 m, con un cuerpo apoyado de masa m = 0.30 kg. Al ser liberado del cuerpo desde el reposo se produce un ascenso vertical.
a) ¿Qué módulo tiene la velocidad del cuerpo al despegarse del resorte?
b) Determina, de forma fundamentada, y explica si el cuerpo llega a pegar en el techo que está a una altura de 3 m desde el suelo en el que apoya el resorte de un 1 m de longitud cuando está en reposo.
-
Aplicación del principio de conservación de la energía a un sistema con rozamiento (5973)
Un bloque de 2.0 kg inicialmente a 0.8 m de altura, comprime inicialmente 10 cm a un resorte de constante k = 600 N/m hasta que sale liberado del mismo. En la parte más baja ingresa a una región donde existe una fuerza de rozamiento de módulo variable, como se ve en la gráfica de la figura.
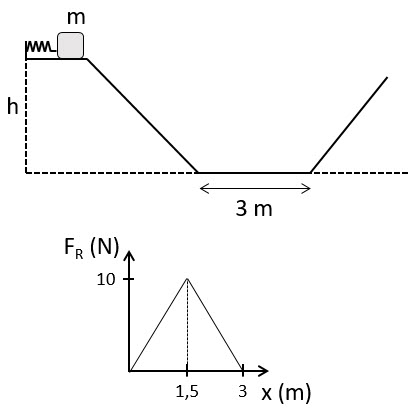
Energía potencial elástica
a) En función de los datos anteriores, calcula la máxima altura que alcanzará la masa.
b) ¿Volverá a atravesar toda la zona con rozamiento? Justifica tu respuesta.
Energía potencial elástica
Ejercicios FyQ