Posición

(64) ejercicios de Posición

(#6159) Seleccionar

Posición, velocidad y momento angular de un sistema de dos partículas distintas (6159)

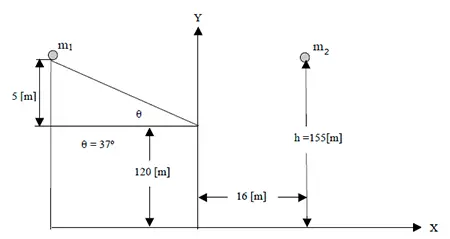
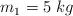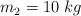Las partículas $m_1 = 5\ kg$ y $m_2 = 10\ kg$ tienen movimientos independientes. La partícula 1 se deja libre sobre el plano liso, inclinado un ángulo 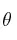$\theta$ , mientras que la partícula 2 se lanza verticalmente hacia abajo desde la altura h con una velocidad inicial de 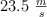$23.5 \ \textstyle{m\over s}$ . La partícula 2 inicia su movimiento en el instante en que la partícula 1 abandona el plano inclinado. Determina, para t = 2 s después de que la partícula 1 abandona el plano inclinado:

a) La posición del centro de masas del sistema constituido por 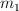$m _1$ y $m _2$ .

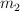b) La velocidad del centro de masas.

c) El momento angular de cada partícula respecto al origen del sistema de referencia.

Posición
(#6158) Seleccionar

Posición, velocidad y momentos angular y lineal de un sistema de dos partículas (6158)

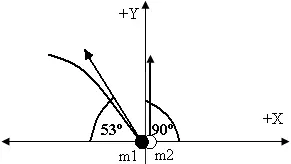
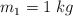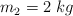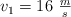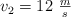La figura muestra un sistema formado por dos partículas con masas $m_1 = 1\ kg$ y $m_2 = 2\ kg$ . Las partículas se lanzan simultáneamente y sus velocidades iniciales son $v_1 = 16\ \textstyle{m\over s}$ y $v_2 = 12\ \textstyle{m\over s}$ . Para el instante t = 2 s, determina:

a) La posición del centro de masas del sistema respecto al origen.

b) La velocidad del centro de masas del sistema respecto al origen.

c) El momento angular del sistema respecto al origen.

d) El momento lineal de la partícula 1 respecto al centro de la masas.

Posición
(#6114) Seleccionar

Refuerzo: objeto se mueve dentro de un tren que se desplaza con aceleración (6114)

En el interior de un tren, que parte del reposo y acelera con 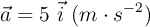$\vec a = 5\ \vec i\ (m\cdot s^{-2})$ , un objeto se desliza por el suelo del tren sin rozamiento con 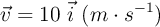$\vec v = 10\ \vec i\ (m\cdot s^{-1})$ respecto a tierra.

a) ¿Cómo es el movimiento del objeto para un observador que va en el tren? ¿Por qué?

b) ¿Qué tiempo transcurrirá para que el objeto alcance nuevamente su posición original con respecto al vagón?
(#6095) Seleccionar

Aceleración, posición y velocidad de un cuerpo con movimiento uniformemente acelerado (6095)

Un cuerpo que se encontraba inicialmente reposo comienza a moverse en línea recta y con aceleración constante y al cabo de 5 s adquiere una velocidad de 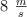$8 \ \textstyle{m\over s}$ . A partir de esta situación, calcula:

a) La aceleración del cuerpo.

b) La posición del cuerpo al cabo de 5 s.

c) La velocidad del cuerpo después de 8 s.
(#6025) Seleccionar

Velocidad, rapidez y posición de una partícula a partir de su aceleración (6025)

En t = 0, una partícula parte del reposo en x = 5 m e y = 8 m, y se mueve en el plano XY con una aceleración de 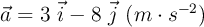$\vec{a} = 3\ \vec{i} - 8\ \vec{j}\ (\textstyle{m\cdot s^{-2}})$ . Determina:

a) Las componentes X e Y de la velocidad en t = 4 s.

b) La rapidez de la partícula en t = 4 s.

c) La posición de la partícula en t = 8 s.