-
Velocidad con la que se mueven dos carros que chocan y quedan unidos (5481)
Un carrito de 8 kg que se mueve con una velocidad de 5 m/s choca con otro carrito de 2 kg que se encuentra en reposo y después del choque los dos carritos siguen moviéndose juntos. ¿Cuál es la velocidad final de los dos carros?
-
Velocidad angular de un sistema tras un choque inelástico (5211)
Una partícula de masa m con rapidez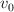 
impacta sobre un extremo de una barra de longitud L, que se encuentra en reposo y que puede girar libremente en torno al extremo opuesto al del impacto. Después del choque, la partícula queda incrustada en la barra y el sistema partícula-barra se detiene cuando el extremo del impacto alcanza una altura de L/2. Determina:
a) La velocidad angular de la barra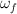 
un instante después del choque.
b) La velocidad 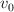de la partícula antes del choque.
-
Velocidad final tras la colisión ineslástica de un camión y dos coches (5077)
Un camión de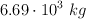 
se dirige hacia el este a 41.0 km/h cuando colisiona simultáneamente con dos carros en una de las intersecciones de la carretera. Uno de los carros es de 
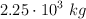y viaja hacia el norte a 102 km/h, el otro carro es de 
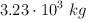y viaja hacia el oeste a 98.0 km/h. Suponiendo que los tres vehículos quedan unidos después de la colisión, determina:
a) ¿Cuál es la velocidad de los carros y el camión justo después de la colisión?
b) ¿Cuál es la dirección justo después de la colisión?
c) Realiza un diagrama donde se evidencie la situación antes y después de la colisión.
-
Conservación de energía: choque inelástico bala-bloque (3789)
Una bala de 0.01 kg que se mueve horizontalmente golpea un bloque de madera de masa 1.5 kg suspendida de un hilo de 2 m de longitud. La bala se incrusta en la madera y éste sube una altura de 0.40 m. ¿Cuál era la velocidad de la bala en el instante anterior a golpear el bloque de madera?
-
Choque inelástico y transformación de energía (3295)
Un bloque de 500 g se encuentra en reposo sobre una superficie horizontal sin rozamiento y unido a un resorte de constante elástica k = 300 N/m, cuando una bala de 5 g lo impacta con una velocidad de 1 000 m/s. Calcula:
a) ¿Cuál será la velocidad del bloque inmediatamente después del impacto?
b) ¿Cuál será la compresión máxima del resorte?
Choque inelástico
Ejercicios FyQ