-
Velocidad y aceleración de un lanzamiento vertical hacia arriba (233)
Un proyectil es disparado verticalmente hacia arriba según la ecuación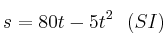 
. Calcula:
a) La ecuación de su celeridad.
b) Su aceleración.
c) El instante en el que su velocidad es nula.
-
Aceleración tangencial, normal y total de un tren que circula por una vía circular (232)
Un tren parte del reposo por una vía circular de 400 m de radio y se mueve con un movimiento uniformemente acelerado hasta que, a los 25 s de iniciada su marcha, alcanza la velocidad de 36 km/h, siendo constante a partir de ese momento. Calcula:
a) La aceleración tangencial en la primera etapa del movimiento.
b) La aceleración normal en el instante t = 25 s.
c) La aceleración total en dicho instante.
-
Velocidad y aceleración a partir de la ecuación de posición (231)
La ecuación del movimiento de un sistema es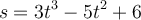 
(SI). Calcula la celeridad del sistema en función del tiempo y el valor de esta en el instante 2 s, además de la aceleración tangencial en función del tiempo y su módulo en el instante 3 s.
-
Aceleración que sufren los pasajeros de una atracción de feria que gira (63)
Una atracción de feria gira a 15 vueltas por minuto. Si el diámetro de la atracción es de 15 m, ¿qué aceleración soportan los pasajeros? ¿Cuánto vale esa aceleración?
-
Aceleración de una rueda a partir de su velocidad angular y su perímetro (62)
La rueda de una bicicleta tiene un perímetro de 3.77 m y gira a 50 rpm. ¿Cuál será la velocidad que lleva la bicicleta, expresada en km/h? ¿Cuánto será la aceleración de la rueda?
Aceleración
Ejercicios FyQ