-
Concentraciones de los componentes de una mezcla de disoluciones (8460)
Se prepara una disolución mezclando 50.0 g de sulfato de cobre(II) pentahidratado (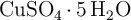
) con 200 mL de una disolución acuosa de 
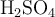1.50 M, cuya densidad es 1.12 g/mL. Posteriormente, se diluye la mezcla hasta un volumen final de 500 mL, obteniendo una disolución con una densidad de 1.18 g/mL. Calcula:
a) La molaridad de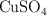 
en la disolución final.
b) La molalidad de 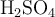en la disolución final.
c) El porcentaje en masa de 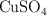en la disolución final.
d) La fracción molar de agua en la disolución final.
Datos: Cu = 63.55, S = 32.07, O = 16.00, H = 1.01. Considera que el 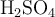se disocia completamente en sus iones.
-
Constante de velocidad y tiempo de vida media para una reacción de primer grado (8459)
Se ha estudiado la descomposición del compuesto «A» en productos a una temperatura constante de 298 K. La reacción es de primer orden respecto a «A». A continuación, se proporcionan los datos experimentales de la concentración de «[A]» en función del tiempo:
![\begin{tabular}{| c | c |} \hline tiempo\ (s) & [A]\ (\text{mol}\cdot L^{-1}) \\\hline 0&1.000\\\hline 50&0.607\\\hline 100&0.368\\\hline 200&0.135\\\hline 300&0.050\\\hline \end{tabular}](local/cache-TeX/3d221adca24eb6004ced5083ef82c57a.png "\begin{tabular}{| c | c |} \hline tiempo\ (s) & [A]\ (\text{mol}\cdot L^{-1}) \\\hline 0&1.000\\\hline 50&0.607\\\hline 100&0.368\\\hline 200&0.135\\\hline 300&0.050\\\hline \end{tabular}")
Determina la constante de velocidad de la reacción «k», utilizando la regresión lineal como método gráfico, y el tiempo de vida media de la reacción.
-
Análisis dimensional de la fuerza «centrígufa» en un sistema no inercial (8458)
En mecánica, la fuerza «centrífuga» en un sistema rotatorio no inercial se expresa como:
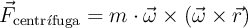
donde: «m» es la masa de la partícula (en kg), «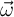
» es la velocidad angular y «
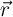» es el vector de posición, todas la magnitudes expresadas en unidades SI.
a) Determina las dimensiones de la fuerza «centrífuga» y verifica que coincidan con las de una fuerza.
b) Si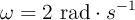 
y r = 0.5 m, calcula el módulo de la fuerza «centrífuga» para una masa de 3 kg.
-
Velocidad y aceleración de un móvil en función del tiempo (8457)
Un móvil describe una trayectoria en el plano XY dada por el vector de posición, expresado en unidades SI:
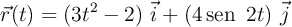
a) Determina los vectores velocidad y aceleración en función del tiempo.
b) Calcula los vectores velocidad y aceleración en el instante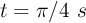 
.
c) Halla el módulo de la velocidad y de la aceleración en .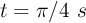
-
Constante de desintegración y actividad radiactiva de la desintegración alfa del radio (8455)
Un núcleo de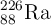 
(radio-226) experimenta desintegración 
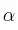con una vida media 
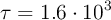años, transformándose en 
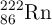(radón-222).
a) Escribe la reacción nuclear correspondiente a este proceso.
b) Calcula la constante de desintegración (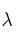
), expresada en 
.
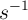c) Determina la actividad inicial de una muestra de 1.00 g de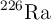 
.
d) ¿Cuánto tiempo tardará la muestra en reducir su actividad al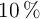 
del valor inicial, expresado en años?
Datos: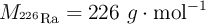 
; 
.
RESUELTO
Ejercicios FyQ