-
Aceleración de un sistema de tres bloques unidos por cuerdas (5918)
Un bloque de 100 g descansa sobre otro de 900 g, siendo arrastrado el conjunto con velocidad constante sobre una superficie horizontal, merced a la acción de un cuerpo de 100 g que cuelga suspendido de un hilo. Si el primer bloque de 100 g lo separamos del de 900 g y lo unimos al bloque suspendido, el sistema adquiere una cierta aceleración en el sentido indicado.
a) Calcula el valor de esta aceleración.
b) ¿Cuál es la tensión de las dos cuerdas?
-
Aceleración de un conjunto de dos cuerpos enlazados con rozamiento (5908)
La imagen presenta dos masas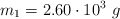 
y 
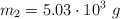unidas por una cuerda que pasa por una polea sin fricción y masa despreciable. La masa 
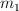se encuentra sobre una superficie rugosa.
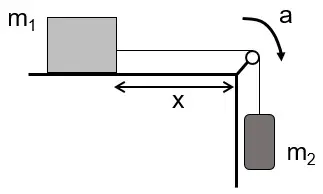
Cuerpos enlazados
a) Realiza un diagrama de fuerzas para cada masa.
b) Expresa la aceleración del sistema en términos de las masas y el coeficiente de fricción cinética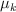 
.
c) Halla el valor de la aceleración, tomando como valor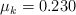 
.
d) Si el bloque 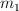se encuentra a una distancia x = 0.961 m, ¿cuánto tardará en llegar a la esquina de la mesa?
e) ¿Cuál debería ser la masa mínima de 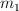para que el sistema quede en reposo? Toma el valor del coeficiente de fricción estático como 
.
-
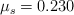Tensión de la cuerda que une dos cuerpos en equilibrio (5890)
Un cuerpo de 30 N de peso está sobre la superficie de un plano inclinado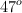 
sobre la horizontal y enlazado con una cuerda inextensible y de masa despreciable a otro cuerpo de 45 N de peso suspendido verticalmente al otro lado del plano. Si el sistema está en equilibrio, ¿cuál es la tensión de la cuerda?
-
Coeficiente de rozamiento cinético de un sistema de tres masas enlazadas (5877)
Un sistema de tres masas como el que se muestra en la figura se utiliza como dispositivo para determinar el coeficiente de fricción cinético entre la masa y la superficie horizontal:
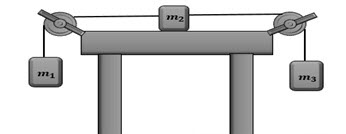
Cuerpos enlazados
a) Determina el valor del coeficiente de fricción cinético entre la superficie horizontal y la masa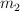 
, teniendo en cuenta que los valores de las masas 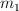, 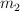y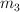 
son de 2.00 kg, 3.40 kg y 8.00 kg respectivamente y la aceleración del sistema es de 
.
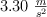b) Determina el valor de las tensiones de las dos cuerdas.
NOTA: En todos los cálculos se asume que no hay fricción en las poleas y que la cuerda es inextensible.
-
Aceleración de un sistema de dos cuerpos enlazados y tensión de la cuerda que los une (5604)
Un cuerpo de 40 kg de masa descansa sobre una mesa mediante una cuerda que pasa por una polea y se une a otro de 30 kg que cuelga libremente. Calcula la aceleración de los cuerpos y la tensión de la cuerda suponiendo que el coeficiente de rozamiento para el cuerpo vale 0.2.
Cuerpos enlazados
Ejercicios FyQ