-
Teorema de conservación de la energía mecánica aplicado a un resorte que se comprime (6519)
El sistema masa-resorte que se presenta a continuación tiene las siguientes características.
– Masa del bloque: 0.658 kg.
– Velocidad en el punto a): 1.15 m/s.
– Constante de la elasticidad del resorte: 58.0 N/m.
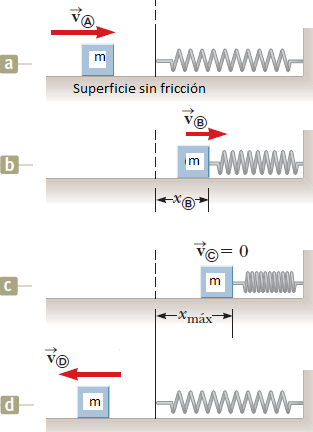
Energía cinética
A partir de la anterior información y basándote en el teorema de conservación de la energía mecánica:
i) Expresa la energía mecánica en cada situación, justificando la respuesta.
ii) Calcula el valor de la comprensión del resorte en c (compresión máxima).
iii) Calcula el valor de la velocidad en d.
iv) Calcula el valor de la velocidad en b asumiendo que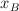 
es la mitad de la compresión máxima del resorte.
-
Velocidad y dirección de un seguidor de línea tras un choque
En una demostración de robots seguidores de línea, dos seguidores de línea se deslizan sobre una superficie sin fricción. El primer seguidor, con masa de 20.0 g, se mueve inicialmente a 1.58 m/s paralelo al eje X, y choca con el segundo seguidor, cuya masa es de 13.0 g que está inicialmente en reposo. Después del choque, el primer seguidor se mueve a 0.93 m/s en una dirección que forma un ángulo de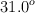 
con su dirección inicial. A partir de la información anterior, determina:
a) La velocidad final que tiene el segundo seguidor.
b) ¿La dirección del segundo seguidor justo después del choque con respecto al eje X positivo?
c) La energía cinética total y antes después del choque y verifique si el teorema de conservación de la energía cinética se cumple o no.
-
Conservación de la energía cuando una esfera choca contra un resorte (6466)
En una práctica, una esfera de masa 1.98 kg que se desliza por una pista horizontal lisa (sin fricción) con una velocidad de 1.26 m/s y choca con un resorte de masa despreciable y constante k = 528 N/m en equilibrio y con uno de sus extremos fijo. A partir de la información anterior, calcula:
a) La distancia que se comprime el resorte.
b) La altura desde la que debería caer la esfera sobre el resorte, si este se coloca verticalmente, para producir la misma compresión del apartado anterior, asumiendo que en ese punto la esfera se detiene.
-
Velocidad final de un protón cuando se le acerca un núcleo de oro (6448)
Un núcleo de oro está a 100 fm de un protón en reposo. Cuando se libera el protón, adquiere una velocidad debido a la repulsión que le produce la carga del núcleo de oro. Calcula la velocidad del protón después de recorrer una gran distancia.
Datos: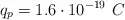 
; 
-
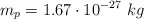
Energía cinética de un carro sabiendo masa y velocidad (6404)
Determina la energía cinética de un carro de 70 kg que viaja a una velocidad de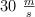 
.
Energía cinética
Ejercicios FyQ