-
Conservación de la energía para un péndulo balístico (6666)
Una esfera de masa M pende sostenida por una barra rígida de masa despreciable y largo L. Una bala de masa m se dispara horizontalmente contra la esfera y la atraviesa. Al salir, la bala tiene la mitad de la rapidez que tenía antes de entrar y continúa su trayectoria recta. Llamando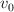 
a la rapidez de la bala al impactar, encuentra:
a) La rapidez de la masa M, inmediatamente después del choque.
b) La rapidez mínima con que debe impactar la bala a la esfera para que esta realice una trayectoria circular completa tras ser atravesada por la bala.
-
Cuerpo lanzado hacia arriba por acción de un resorte comprimido (6657)
Un cuerpo de 2 kg se encuentra sobre un resorte de 1000 N/m de constante que está verticalmente apoyado en el suelo, y comprimido 25 cm. Al destrabar el resorte el cuerpo es impulsado y se separa de él:
a) Indica las fuerzas que actúan a lo largo de su recorrido (posición inicial, una vez destrabado y cuando alcanza la altura máxima), indicando si son conservativas o no conservativas.
b) Halla el trabajo del peso desde la posición inicial hasta alcanzar la altura máxima.
-
Trabajo que realiza el motor de un coche al subir una rampa aumentando su velocidad (6656)
Un coche de 1 000 kg sube 20 m por una rampa de una inclinación de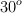 
. La velocidad inicial era de 
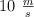y la final de 
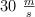. Calcula el trabajo hecho por el motor.
-
Velocidad de una vagoneta a distintas alturas a partir de la deformación del freno (6655)
Una vagoneta de feria de masa de 120 kg se encuentra encima de una pista sin rozamiento. El tramo inicial de la pista es horizontal. A medio camino, la pista hace una subida hasta un segundo tramo horizontal, al final del cual hay un sistema de frenado consistente en un muelle de constante elástica k = 104 N/m. La diferencia de altura entre los dos tramos horizontales es de 4 m. Si el sistema de frenado se comprime 0.8 m, calcula:
a) La velocidad de la vagoneta justo antes de empezar a comprimir el sistema de frenado.
b) La velocidad de la vagoneta justo antes de empezar a subir la rampa.
-
Máxima altura desde la que puede saltar una persona sin romper sus huesos de las piernas (6635)
¿Cuál es la máxima altura desde la que puede saltar una persona de 70 kg, si al llegar al suelo mantiene las piernas rígidas, suponiendo que los huesos de las piernas tienen 0.5 m de longitud y pueden soportar como máximo una deformación unitaria de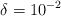 
? Supón que la superficie del hueso en promedio es de 
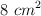y que el módulo de Young de los huesos es 
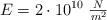. Debes considerar que las articulaciones son infinitamente resistentes de forma que no absorben energía potencial.
Conservación energía
Ejercicios FyQ