-
Análisis del movimiento armónico simple de un partícula (6535)
Una partícula que se mueve describiendo un MAS durante un tiempo de 18 s. Tiene la siguiente ecuación (en unidades SI):
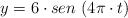
a) Halla el periodo del movimiento.
b) Halla la frecuencia.
c) Halla la elongación (x).
d) Halla el valor de la aceleración.
e) Si duplica el tiempo que tarda para dar una oscilación completa, ¿qué sucede con la elongación?
f) Si cuadruplico el valor de la masa que está oscilando, ¿qué pasa con la velocidad?
-
Periodo, frecuencia y frecuencia angular en un movimiento armónico simple (6472)
Si una partícula da 5 oscilaciones en 10 segundos, halla:
a) Su periodo.
b) Su frecuencia.
c) Su velocidad angular.
-
Tiempo que se adelanta un reloj si se acorta la longitud de su péndulo (6232)
El periodo de un péndulo simple viene dado por la expresión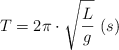 
. Supongamos que la aceleración gravitatoria en el lugar en el que oscila el péndulo es 
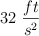. Si el péndulo es el de un reloj que se mantiene sincronizado cuando L = 4 ft, ¿cuánto tiempo se adelantará el reloj en 24 horas si la longitud del péndulo se disminuye hasta los 3.97 ft?
-
Periodo de un péndulo simple en distintos lugares (6115)
Calcula el periodo de un pendulo simple en los siguientes casos:
a) Si su longitud es de 0.556 m, siendo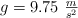 
.
b) En la Luna, con un valor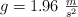 
, si su periodo es de 25 s en un lugar de la Tierra en que 
.
-
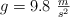Estudio de la posición del péndulo de un reloj y su periodo
El péndulo de un reloj se mueve periódicamente, separándose s (cm) de la vertical. La ecuación que describe el movimiento es:
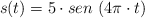
a) Decide a qué distancia de la vertical y de que lado de la misma estará el péndulo a los 2 s.
b) ¿Qué distancia máxima alcanza?
c) ¿En qué instante alcanza la distancia máxima?
d) ¿Cuál es su periodo?
Periodo
Ejercicios FyQ