Dimesiones

(29) ejercicios de Dimesiones

(#7103) Seleccionar

Ampliación: longitud y área de hilo y plancha de oro a partir de su densidad (7103)

El oro tiene una densidad de 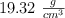$19.32\ \textstyle{g\over cm^3}$ , es el metal más dúctil y puede prensarse en una hoja delgada o estirarse en una fibra larga.

a) Si una muestra de oro, con una masa de 31.65 g, se presiona en una hoja de 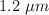$1.2\ \mu m$ de espesor, ¿cuál es el área de la hoja?

b) Si, en cambio, el oro se extrae en una fibra cilíndrica de radio de 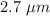$2.7\ \mu m$ , ¿cuál es la longitud de la fibra?
(#6825) Seleccionar

Análisis dimensional para obtener una ecuación de la velocidad de las olas superficiales (6825)

Las olas en la superficie del océano no dependen significativamente de propiedades del agua como la densidad o la tensión superficial. La principal fuerza (fuerza de retorno) para el agua apilada en las crestas de las olas se debe a la atracción gravitacional de la Tierra. Por lo tanto, la rapidez v, expresada en m/s, de las olas oceánicas depende de la aceleración de la gravedad g. Es razonable esperar que v también dependa de la profundidad del agua, h, y de la longitud de onda de la ola (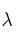 $\lambda$ ). Supón que la rapidez de la ola está dada por la fórmula funcional:

$v = C\cdot g^{\alpha}\cdot h^{\beta}\cdot \lambda^{\gamma}$

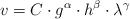
donde 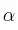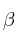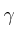$\alpha$ , $\beta$ , $\gamma$ y C son adimensionales. En aguas profundas, el agua por debajo no afecta al movimiento de las olas en superficie, por lo que v debe ser independiente de la profundidad ( 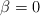$\beta = 0$ ). Utilizando solo análisis dimensional determina una expresión para la rapidez de las olas superficiales en aguas profundas.
(#5948) Seleccionar

Presión y dimensiones de la superficie de un sistema (5948)

¿Cuál es la presión ejercida por una fuerza de 120 N que actúa sobre una superficie de 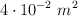$4 \cdot 10^{-2}\ m^2$ ? ¿Cuáles serían las dimensiones de esa superficie si fuera:

a) Cuadrada.

b) Circular.
(#5746) Seleccionar

Velocidad y aceleración de un sistema a partir de la ecuación de posición

La posición de una partícula en función del tiempo está dada por la ecuación 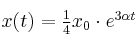$x(t) = \textstyle{1\over 4}x_0\cdot e^{3\alpha t}$ , donde 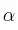$\alpha$ es una constante positiva.

a) ¿En qué instante la posición de la partícula es 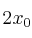$2x_0$ ?

b) ¿Cuál es la rapidez de la partícula en función del tiempo?

c) ¿Cuál es la magnitud de la aceleración de la partícula en función del tiempo?

d) ¿Qué unidades SI tiene 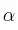$\alpha$ ?
(#5315) Seleccionar

Análisis de unidades y dimensiones (5315)

Si [x] = m, [v] = m/s, [t] = s y [d] = m, encuentra la relación de unidades para cada magnitud:

a) $s = [x]_0 + [v]\cdot [t]$

b) $g = \frac{2[d]}{[t]^2}$

c) $A = [d]^2$

d) $V = \frac{4}{3}[d]^3$