-
Energía potencial de un resorte y trabajo neto realizado (6041)
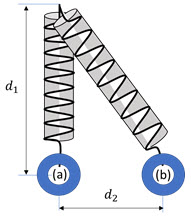
Un niño construye un juguete con un resorte que mide 20 cm de longitud (cuando sobre no se aplica fuerzas externas) y una tapa de 20 cm de diámetro, como se muestra en la figura.
Trabajo
Inicialmente el niño estira el resorte verticalmente 93.8 cm (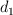
) y luego mueve el juguete horizontalmente 76.5 cm (
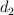), es decir de la posición (a) a la posición (b). Si la constante de elasticidad del resorte es 25.1 N/m, calcula:
a) La energía potencial elástica en la posición (a) y en la posición (b).
b) El trabajo neto realizado.
-
Potencia real y rendimiento de una grúa (6001)
La placa del motor de una grúa indica que tiene una potencia de 3.25 kW. Si el motor tarda 7 s en elevar un objeto de 100 kg hasta una altura de 16 m:
a) ¿Cuál es la potencia real del motor?
b) ¿Coincide la potencia real con la potencia teórica?
c) ¿Cuál es el rendimiento de este motor?
-
Aplicación del principio de conservación de la energía a un sistema con rozamiento (5973)
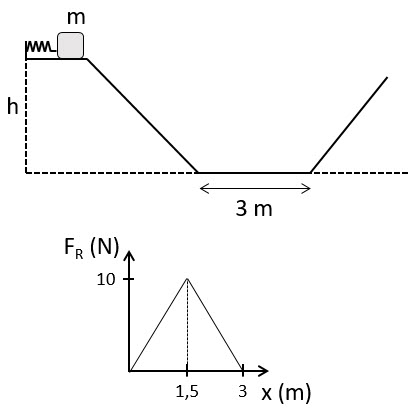
Un bloque de 2.0 kg inicialmente a 0.8 m de altura, comprime inicialmente 10 cm a un resorte de constante k = 600 N/m hasta que sale liberado del mismo. En la parte más baja ingresa a una región donde existe una fuerza de rozamiento de módulo variable, como se ve en la gráfica de la figura.
Trabajo
a) En función de los datos anteriores, calcula la máxima altura que alcanzará la masa.
b) ¿Volverá a atravesar toda la zona con rozamiento? Justifica tu respuesta.
-
Trabajo que realiza el motor de un coche para variar la velocidad
Un vehículo cuya masa es de 950 kg se desplaza por una carretera horizontal a una velocidad constante de 24 m/s. En un momento dado el conductor acelera y alcanza una velocidad de 32 m/s y a partir de este momento continúa con la misma velocidad. Calcula:
a) La energía cinética inicial y final del vehículo.
b) El trabajo realizado por el motor durante el aumento de velocidad.
-
Fuerza que un cuerpo hace sobre la arena cuando cae desde cierta altura
Un cuerpo de 400 g cae desde una altura de 4,0 m sobre un montón de arena. Si el cuerpo llega hasta 3,0 cm de profundidad antes de detenerse. Determina la fuerza que ejercio la arena sobre el.
Trabajo
Ejercicios FyQ