-
Velocidad, periodo y energía de un satélite que orbita la Tierra (8404)
Un satélite artificial de masa 500 kg orbita alrededor de la Tierra en una órbita circular a una altura de 400 km sobre la superficie terrestre. Sabiendo que el radio de la Tierra es de 6 370 km y que la masa de la Tierra es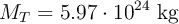 
, calcula:
a) La velocidad orbital del satélite.
b) El período de la órbita.
c) La energía mecánica total del satélite en su órbita.
Dato: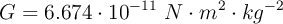 
-
EBAU Andalucía: física (junio 2024) - ejercicio A.1 (8286)
a) Razona si son verdaderos los siguientes enunciados: i) El trabajo total realizado por las fuerzas no conservativas es igual a la variación de la energía mecánica. ii) Siempre que actúen fuerzas no conservativas la energía mecánica varía.
b) Un bloque de masa 150 kg desliza por una superficie horizontal con rozamiento. El bloque se mueve hacia la derecha con velocidad inicial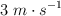 
. Sobre el bloque actúa una fuerza de módulo 20 N dirigida hacia la izquierda y que forma un ángulo de 
sobre la horizontal, recorriendo 25 m hasta detenerse. i) Realiza un esquema de las fuerzas ejercidas sobre el bloque. ii) Calcula las variaciones de energía cinética, potencial y mecánica del bloque en el trayecto descrito. iii) Calcula el trabajo realizado por cada una de las fuerzas aplicadas sobre el bloque.
-
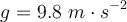
Demostración de la ecuación de la energía mecánica de un satélite (7955)
Demuestra que la energía mecánica que tiene un satélite de masa m en órbita circular alrededor de un planeta de masa M y radio R es:
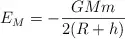
donde h es la altura a la que se halla el satélite de la superficie del planeta.
-
EBAU Andalucía: física (junio 2022) - ejercicio A.1 (7683)
a) i) Define los conceptos de energía cinética, energía potencial y energía mecánica e indica la relación que existe entre ellas cuando solo actúan fuerzas conservativas. ii) Explica razonadamente cómo se modifica dicha relación si intervienen además fuerzas no conservativas.
b) Sobre un cuerpo de 3 kg, que está inicialmente en reposo sobre un plano horizontal, actúa una fuerza de 12 N paralela al plano. El coeficiente de rozamiento entre el cuerpo y el plano es 0.2. Determina, mediante consideraciones energéticas, i) el trabajo realizado por la fuerza de rozamiento tras recorrer el cuerpo una distancia de 10 m, y ii) la velocidad del cuerpo después de recorrer los 10 m.
Dato: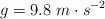 
-
Trabajo que realiza el motor de un coche al subir una rampa aumentando su velocidad (6656)
Un coche de 1 000 kg sube 20 m por una rampa de una inclinación de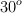 
. La velocidad inicial era de 
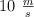y la final de 
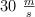. Calcula el trabajo hecho por el motor.
Energía mecánica
Ejercicios FyQ