Momento angular

(13) ejercicios de Momento angular

(#8415) Seleccionar

Posición, velocidad, momento lineal y aceleración del centro de masas de un sistema de dos partículas (8415)

Un sistema de dos partículas de masas 2 y 3 kg se mueven en el plano XY. En un instante dado, las posiciones y velocidades de las partículas son:

$\left \vec{r}_1 = (1, 2)\ (m)\ y\ \vec{v}_1 = (3, -1)\ (m\cdot s^{-1}) \atop \vec{r}_2 = (-2, 1)\ (m)\ y\ \vec{v}_2 = (-1, 4)\ (m\cdot s^{-1}) \right \}$

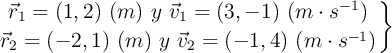
a) Calcula la posición del centro de masas (CM) del sistema.

b) Determina la velocidad del centro de masas.

c) Calcula el momento lineal total del sistema.

d) Determina el momento angular total del sistema respecto al origen.

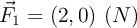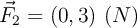e) Si las partículas están sometidas a las fuerzas externas $\vec{F}_1 = (2, 0)\ (N)$ y $\vec{F}_2 = (0, 3)\ (N)$ , calcula la aceleración del centro de masas.
(#7498) Seleccionar

Rueda que gira mientras está sujeta por un eje horizontal (7498)

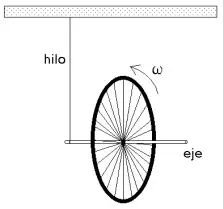
Una rueda de bicicleta se sostiene del eje con una cuerda suspendida del techo tal como muestra la figura.

Momento angular

El punto de amarre se ubica a una distancia de 20 cm del centro de la rueda, la llanta pesa 4 Kg y tiene un radio de 30 cm. La rueda se hace girar a 10 rev/s. El eje se orienta inicialmente de manera horizontal.

a) Demuestra que el eje de la rueda se mantendrá en posición horizontal y que esta realizará un movimiento circular.

b) Calcula la velocidad angular.
(#7380) Seleccionar

Velocidad angular de una atracción para que las personas queden pegadas a la pared (7380)

Una de las atracciones en los parques de diversiones es un cilindro giratorio vertical. Cuando se logra una velocidad de giro lo suficientemente alta las personas dentro del cilindro permanecen pegados a la pared. Durante la rotación la fuerza de fricción estática sostiene a cada persona. Si el radio del cilindro es R= 2 m y coeficiente de fricción entre la persona y la pared del cilindro es de 0.2, ¿cuál es la rapidez angular del cilindro?
(#7341) Seleccionar

Momento angular de un tiovivo con un chico paseando en él (7341)

Una rueda de caballitos tiene un momento de inercia 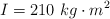$I = 210\ kg\cdot m^2$ y gira alrededor de su eje vertical a 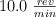$10.0\ \textstyle{rev\over min}$ . En su borde, que dista 1.40 m del eje, está sentado un muchacho de m = 60.0 kg. Calcula el momento angular del sistema rueda-muchacho.
(#7281) Seleccionar

Velocidad angular de una barra homogénea cuando impacta una pelota sobre ella (7281)

Una barra metálica delgada y uniforme, de 2.00 m de longitud y con un peso de 90.0 N, cuelga verticalmente del techo en un pivote sin fricción colocado en el extremo superior. De repente, una pelota de 3.00 kg, que viaja inicialmente a 10.0 m/s en dirección horizontal, golpea la barra 1.50 m abajo del techo. La pelota rebota en dirección opuesta con rapidez de 6.00 m/s. Calcula la rapidez angular de la barra inmediatamente después del choque.